Party Favors
Task
Pia was having a party. She put 10 stickers in each party bag.
- On the first day she made 10 bags. How many stickers were in her 10 bags all together?
- On the second day she made 3 more bags with ten stickers in each one. How many stickers total were in her 10 bags plus 3 more bags?
- On the third day she made 7 more bags with ten stickers in each one. How many stickers total are in her 20 bags of ten?
- On the fourth day, she made another 10 bags with ten stickers in each one. How many stickers are in her 30 bags of ten?
- After one week, she had made a total of 50 bags with ten stickers in each one. How many stickers total are in her 50 bags of ten?
IM Commentary
The point of this task is to emphasize the grouping structure of the base-ten number system, and in particular the crucial fact that 10 tens make 1 hundred. Second graders should have been given opportunities to work with objects and pictures that represent the grouping structure of the base-ten number system, which would help prepare them for doing this task.
This task is meant to be encountered early in the progression for 2.NBT.1, building on some facility with 2.NBT.2.
The task has many parts, especially for this grade level, and while they all establish or use the fact that ten tens is one-hundred, they differ slightly. So one could work on this task in multiple sessions, but one should avoid cutting it short altogether, to more likely engage MP.8 look for regularity in repeated reasoning.
As appropriate, students should be asked to explain their process. Because the task requires a lot of reading, it might be best used as a story that unfolds where the teacher tells the class what happens next and the students figure out what she did each day.
The Standards for Mathematical Practice focus on the nature of the learning experiences by attending to the thinking processes and habits of mind that students need to develop in order to attain a deep and flexible understanding of mathematics. Certain tasks lend themselves to the demonstration of specific practices by students. The practices that are observable during exploration of a task depend on how instruction unfolds in the classroom. While it is possible that tasks may be connected to several practices, only one practice connection will be discussed in depth. Possible secondary practice connections may be discussed but not in the same degree of detail.
This particular task helps illustrate Mathematical Practice Standard 8, Look for and express regularity in repeated reasoning. Second graders will notice and use the understanding that 10 bags of ten stickers make 100 early on in the problem-solving sequence, they will use this same reasoning as they make 20 bags of ten stickers, then 30 bags of ten stickers, and then finally 50 bags of ten stickers. When students are engaged in MP.8, they purposely look for these types of patterns, make conjectures about these patterns, consider generalities and limitations, and make connections over time about their ideas. As they begin to explain their processes to one another, they construct, critique, and compare arguments (MP.3).
Solution
-
With the help of a picture such as the following:
one can count by tens to see that ten groups of ten prizes is one-hundred prizes.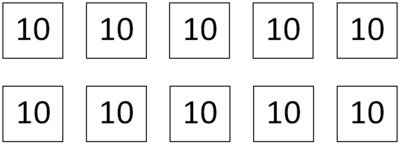
- There are two main possible approaches. One can either add three bags to the picture above and continue to count. Or one can notice that the three new bags constitute 30 prizes, and since there were already 100 that would make 130 prizes.
- Since we counted that ten boxes of ten is one hundred, twice that would be two hundreds, or 200.
- Ten boxes of ten is 100 more. Since we had 200 – or two hundreds – before, adding one more hundred will give three hundreds, or 300.
- Fifty boxes of ten can be broken up into five collections of ten boxes of ten. Since ten boxes of ten is 100, five of those is five hundreds, or 500.
Party Favors
Pia was having a party. She put 10 stickers in each party bag.
- On the first day she made 10 bags. How many stickers were in her 10 bags all together?
- On the second day she made 3 more bags with ten stickers in each one. How many stickers total were in her 10 bags plus 3 more bags?
- On the third day she made 7 more bags with ten stickers in each one. How many stickers total are in her 20 bags of ten?
- On the fourth day, she made another 10 bags with ten stickers in each one. How many stickers are in her 30 bags of ten?
- After one week, she had made a total of 50 bags with ten stickers in each one. How many stickers total are in her 50 bags of ten?
