Task
The picture below is called a Venn Diagram. Each circle (A, B, and C) contain shapes that all share at least one characteristic. Some shapes are contained in more than one circle because they share more than one characteristic. For example, shape 3 fits the rule for circles A and B, but not circle C. It lies within circles A and B, but not circle C.
- What are the characteristics shared by shapes within circle A? Within circle B? Within circle C? Double check to make sure that any shapes that have that characteristic are contained within the circle and any shapes that don't lie outside of the circle.
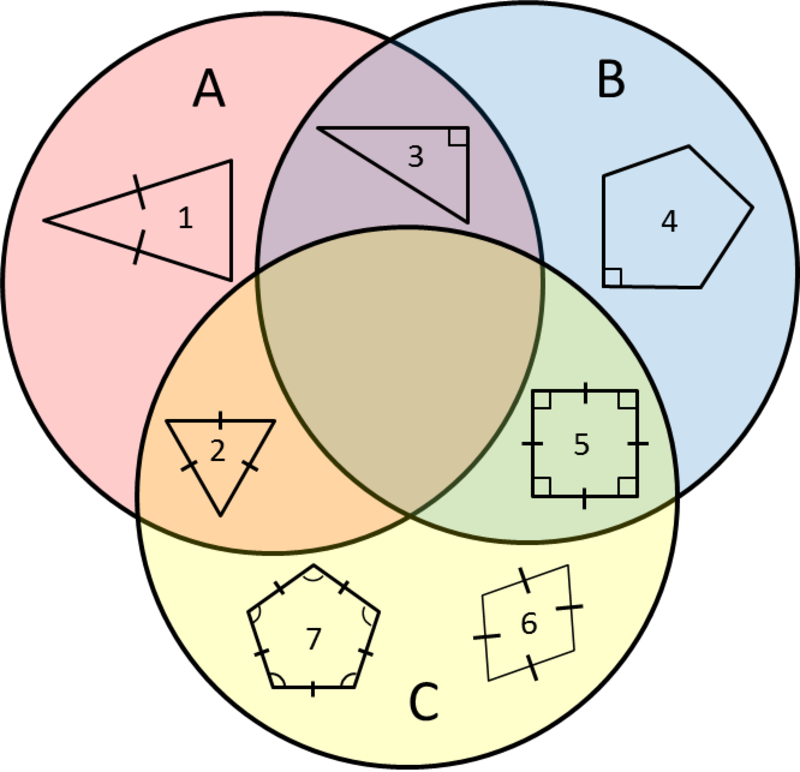
Characteristics of all shapes contained in Circle A:
Characteristics of all shapes contained in Circle B:
Characteristics of all shapes contained in Circle C:
b. Where would you place a rectangle that does not have four sides of the same length? Why?
IM Commentary
This task asks students to classify shapes based on their properties. The task itself is straightforward, but there are a number of opportunities to present this task in class and push the level of discussion and reasoning. For example, the rule for the bottom circle is that all shapes must have all sides with the same length. Some students will likely conjecture that the rule is either that all shapes must be regular polygons or that all shapes must be equiangular. Either of these would be true except for the rhombus.
Though this would likely extend beyond the scope of 5th grade understanding, it might be interesting to look at the pentagon with the right angle. In the eyes of a 5th grader, it looks as if it might have sides of equal length. They have not yet derived any rules about the sum of interior angles in polygons, but they should be pushed to see that mathematicians cannot make assumptions based on the appearance of shapes. We only know that each of the shapes in the bottom circle is equilateral because the tick marks indicate that the sides are the same length. In that same line of reasoning, we must be careful to specify in part b that the rectangle does not have equal sides. A deep discussion would allow students to construct viable arguments and critique the reasoning of others (MP 3) and attend to precision (MP 6).
Though this task is written to address the 5th grade standards, it can be adapted for the 8th grade geometry standards. A challenge question that extends beyond the scope of the 5th grade standards would be: What kind of shape could go in the center of this Venn Diagram? Be specific about its properties. If there could not be a shape that belongs in the center, justify your reasoning.

