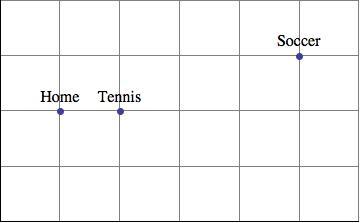
Task
The Jonas family had a really busy day. After leaving their home, Mrs. Jonas dropped son Cody at his tennis practice. She then drove daughter Kristin to her soccer game and stayed to watch. After the game, mother and daughter picked up Cody on the way home. Once home, Mrs. Jonas saw that they had driven 20 miles that day. How far are the tennis courts from home?
- Use any method you like to find the distance between the tennis courts and home.
- Set up and solve an equation in one variable to find the distance between the tennis courts and home.
Note: The family car can only travel along the main streets (gridlines), and all distances between cross streets are the same distance. Assume Mrs. Jonas took the most direct routes to and from her destinations.
IM Commentary
This problem can be solved using simple arithmetical reasoning but is also naturally represented by a simple equation. Thus, it provides a good entry point for students into representing quantities in contexts with variables and expressions and building equations that reflect the relationships presented in the context.
In order for this task to fulfill its instructional promise, students are first asked to solve the problem themselves in any way they see fit. They could then explain their solution strategy to a partner, giving everyone a chance to articulate their reasoning. The teachers might circulate around the room and ask students with different ways of representing the problem to present their approach to the class, starting with the least abstract and ending with the most abstract. If no students use an equation to represent the problem in the first part, they are specifically asked to set up and solve an equation in the second part of the task. Finally, students should be given opportunities to work on problem contexts such as 6.EE Morning Walk where an algebraic approach is both grade-appropriate and clearly more efficient. This will help them see the value of a symbolic approach.
One advantage to using this task to introduce the idea of a variable is that the unknown has a natural visual representation, namely the length of the segments between gridpoints, in particular, the distance between home and the tennis courts.
An extension to this task could be to ask the students: What other questions could you ask about this situation? Some possibilities are:
- How far is it from the tennis courts to the soccer field?
- How many different routes can Mrs. Jonas take on her trip?
- How long does the trip take if we assume an average speed of 35 miles per hour?

