Computing Volume Progression 3

Task

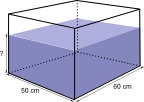
A rectangular tank is $50\text{ cm}$ wide and $60\text{ cm}$ long. It can hold up to $126$ $\ell$ of water when full. If Amy fills $\frac23$ of the tank as shown, find the height of the water in centimeters. (Recall that $1$ $\ell = 1000\text{ cm}^3$.)

IM Commentary

This is the third in a series of four tasks that gradually build in complexity. The purpose of this series of tasks is to build in a natural way from accessible, concrete problems involving volume to a more abstract understanding of volume. Here, we are given the volume and are asked to find the height. In order to do this, students must know that $1$ $\ell = 1000$ $cm^3$. This fact may or may not need to be included in the problem, depending on students’ familiarity with the units.

Solution

First, find the volume of tank in cubic centimeters:

$$126 \ell \times \frac{1000\text{ cm}^3}{1 \ell} =126 \times1000\text{ cm}^3 .$$ The height of tank is the volume divided by the length and the width: $$\frac{126 \times 1000}{50 \times 60} = 42\text{ cm}.$$ The height of water is $\frac23$ the height of the tank: $$\frac23 \times 42 = 28.$$ So the height of the water is $28\text{ cm}$.