Rounding and Subtracting
Task
Xiaoli was estimating the difference between two positive numbers $x$ and $y$ (where $x\gt y$). First she rounded $x$ up by a small amount. Then she rounded $y$ down by the same amount. Finally, she subtracted the rounded values. Which of the following statements is correct?
- Her estimate is larger than $x-y$.
- Her estimate is smaller than $x-y$.
- Her estimate equals $x-y$.
- Her estimate equals $y-x$.
- Her estimate is $0$.
- There is not enough information to compare $x-y$ with her estimate.
IM Commentary
This task addresses what happens to rounding discrepancies when arithmetic is performed on rounded numbers and would be a good problem for classroom discussion. This is an important aspect of precision (MP6) and it is good for students to gain early exposure to this kind of work. For students who do well on this task, the teacher might ask them to consider what would happen, in the same scenario, to the sum $x + y$ compared to the sum of the rounded numbers or similarly for the products.
Two different solutions are given. The first uses a number line to give a visual representation as appropriate for 7th grade. The second takes an algebraic approach, and reflects the kind of reasoning students might demonstrate in high school. The second approach requires comfort dealing with several variables; one way to scaffold this approach would be to suggest to students that they use specific values for $x$ and $y$ instead of variables.
This task was adapted from problem #6 on the 2012 American Mathematics Competition (AMC) 10B Test. For the 2012 AMC 10B, which was taken by 35,086 students, the multiple choice answers for the problem had the following distribution:
| Choice | Answer | Percentage of Answers |
| (A)* | Her estimate is larger than $x-y$. | 65 |
| (B) | Her estimate is smaller than $x-y$. | 8 |
| (C) | Her estimate equals $x-y$. | 12 |
| (D) | Her estimate equals $y-x$. | 2 |
| (E) | Her estimate is $0$. | 3 |
| Omit | -- | 10 |
Of the 35,086 students, 17,169 or 49% were in 10th grade, 9,928 or 28% were in 9th grade, and the remainder were below than 9th grade.
Solutions
Solution: 7.NS Looking at quantities on a number line
Below is a depiction of the number line for this problem. Note that $x$ has been rounded up by a small amount to a point labeled $a$, and $y$ has been rounded down (by the same amount) to a point labeled $b$:

In this picture, $x - y$ is the distance between $x$ and $y$ on the number line while $a - b$ is the distance between $a$ and $b$ on the number line.
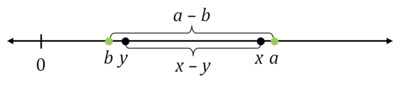
We can see that the interval between $a$ and $b$ contains the interval between $x$ and $y$ so this means that $a - b \gt x - y$. So Xiaoli's estimate for $x - y$ will be too large.
Solution: N-RN A high school level explanation of the same principle
We will call $a$ the amount Xiaoli has rounded $x$ to and $b$ the amount to which she rounds $y$. We are given that $a$ is bigger than $x$ so $a - x \gt 0$. We are also given that $b$ is less than $y$ so $y - b \gt 0$. We are actually given that $a -x = y - b$ though we will not need this to answer the question. In order to compare $a-b$ to $x-y$ we will first write $a$ in terms of $x$ and $b$ in terms of $y$. We have $$ a = x + (a-x) $$ and we know that $a-x$ is positive. We similarly have $$ b = y + (b - y) $$ and we know that $b-y$ is negative.
We can now calculate to compare $a - b$ to $x - y$
The second line uses arithmetic to rearrange terms and the third line uses the assumption that $a-x$ and $y-b$ are both positive.
Rounding and Subtracting
Xiaoli was estimating the difference between two positive numbers $x$ and $y$ (where $x\gt y$). First she rounded $x$ up by a small amount. Then she rounded $y$ down by the same amount. Finally, she subtracted the rounded values. Which of the following statements is correct?
- Her estimate is larger than $x-y$.
- Her estimate is smaller than $x-y$.
- Her estimate equals $x-y$.
- Her estimate equals $y-x$.
- Her estimate is $0$.
- There is not enough information to compare $x-y$ with her estimate.
