Eva is using the green triangle, since two of the vertices of the triangle are at $(0,0)$ and $(3,2)$. She will next find the length of each leg in the right triangle. The horizontal leg length is the difference between the $x$-coordinates, which is 3. The vertical leg length is the difference between the $y$-coordinates, which is 2. So the line rises by 2 units for every horizontal increase of 3 units. Therefore the slope is $\frac{2}{3}$.

Carl is using the blue triangle, since two of the vertices of the triangle are at $(3,2)$ and $(6,4)$. He will next find the length of each leg in the right triangle. The horizontal leg length is the difference between the $x$-coordinates, which is 3. The vertical leg length is the difference between the $y$-coordinates, which is 2. So the line rises by 2 units for every horizontal increase of 3 units. Therefore the slope is $\frac{2}{3}$.
Maria is using the red triangle, since two of the vertices of the triangle are at $(3,2)$ and $(9,6)$. She will next find the length of each leg in the right triangle. The horizontal leg length is the difference between the $x$-coordinates, which is 6. The vertical leg length is the difference between the $y$-coordinates, which is 4. So the line rises by 4 units for every horizontal increase of 6 units. Therefore, the slope is $\frac{4}{6}$.
To compute the slope between two points, we are computing the quotient of the lengths of the legs in a right triangle. We can see that the blue and the green triangles are congruent since we can translate the green triangle along the line until it lines up with the blue triangle. Therefore, the quotient of the lengths of the legs must be the same.

The red triangle is not congruent to the blue triangle but it is similar to it. We can dilate the blue triangle by a factor of 2 to line it up with the red triangle. The sides in similar triangles also have the same proportion. Therefore, the quotient of the lengths of the legs of the two triangles must be the same.

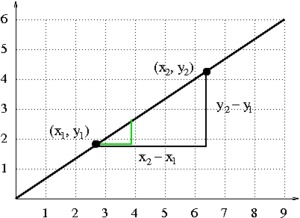
Parts (a) and (b) suggest the following picture:

The lengths of the vertical leg of this triangle is $y_2-y_1,$ and the length of the horizontal leg is $x_2-x_1$.
The slope between these two points is the quotient of these two lengths: $\frac{y_2-y_1}{x_2-x_1}$.
This slope should be the same as the slope obtained by Eva because her green triangle is similar to the triangle we drew above. To see this,
- First, translate Eva's triangle $x_1$ units to the right and $y_1$ units up. Now the two triangles share a vertex.


- Next, dilate Eva's triangle by a factor of $\frac13$ (so the horizontal leg has a length of 1) and then by a factor of $x_2-x_1$ (so the horizontal leg has a length of $x_2-x_1$). Use the common vertex as the center of the dilation.

Because angles are preserved by translations and dilations, this shows that Eva's triangle and our triangle are similar and that the legs are proportional. So
$$\frac{y_2-y_1}{x_2-x_1}=\frac23$$
and the slope is the same no matter which two points on this line we choose to compute with.










