Find the Angle
Task
In triangle $\Delta ABC$, point $M$ is the point of intersection of the bisectors of angles $\angle BAC$, $\angle ABC$, and $\angle ACB$. The measure of $\angle ABC$ is $42^\circ$, and the measure of $\angle BAC$ is $64^\circ$. What is the measure of $\angle BMC$?
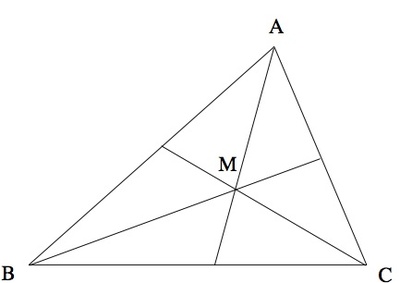
This task adapted from a problem published by the Russian Ministry of Education.
IM Commentary
The task is an example of a direct but non-trivial problem in which students have to reason with angles and angle measurements (and in particular, their knowledge of the sum of the angles in a triangle) to deduce information from a picture.
This task includes an experimental GeoGebra worksheet, with the intent that instructors might use it to more interactively demonstrate the relevant content material. The file should be considered a draft version, and feedback on it in the comment section is highly encouraged, both in terms of suggestions for improvement and for ideas on using it effectively. The file can be run via the free online application GeoGebra, or run locally if GeoGebra has been installed on a computer.
Some notes on the use of the GeoGebra file: The file gives the proctor of the problem the abilty to set 2 of the 3 angles before showing the problem to the student. It would also allow for a student or group to use this to evaluate a specific instance of the problem. Also, a teacher could load this on multiple computers where groups or students could move from station to station to have a variety of problems. Once the angles are set, the problem appears and the student is allowed to enter what they think the third angle should be. A popup alerts the student if they are correct or incorrect. There is a check box that shows the solution with a graphical explanation. From there, you can reset the problem to its initial state.
Attached Resources
Solution
All angle measurements are in degrees.
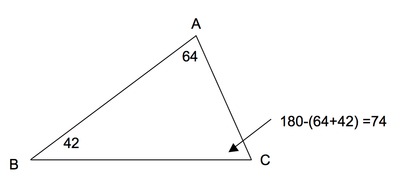
The solution is obtained by applying the Triangle Sum Theorem twice. First apply it to the triangle $ABC$ to find the measure of angle $ACB$. This angle has measure $180^\circ -(64^\circ +42^\circ )=180^\circ -(106^\circ)=74^\circ$:
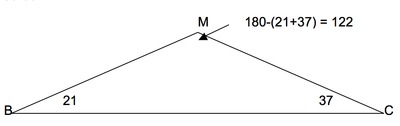
Now consider the triangle $BMC$. Since the segment $BM$ bisects the angle $ABC$ of the triangle, we have the measure of angle $MBC$ is half the measure of angle $ABC$, which is half of $42^\circ$, or $21^\circ$. Similarly, the measure of angle $MCB$ is half of angle $ACB$, which is half of $74^\circ,$ which is $37^\circ$. Now use the Triangle Sum Theorem on the triangle $BMC$ to find that the measure of angle $BMC$ is $180^\circ - (37^\circ+21^\circ)=180^\circ-58^\circ=122^\circ:$
Find the Angle
In triangle $\Delta ABC$, point $M$ is the point of intersection of the bisectors of angles $\angle BAC$, $\angle ABC$, and $\angle ACB$. The measure of $\angle ABC$ is $42^\circ$, and the measure of $\angle BAC$ is $64^\circ$. What is the measure of $\angle BMC$?

This task adapted from a problem published by the Russian Ministry of Education.
