Glasses
Task
The diagram shows three glasses (not drawn to scale). The measurements are all in centimeters.
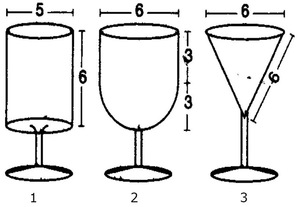
The bowl of glass 1 is cylindrical. The inside diameter is 5 cm and the inside height is 6 cm.
The bowl of glass 2 is composed of a hemisphere attached to cylinder. The inside diameter of both the hemisphere and the cylinder is 6 cm. The height of the cylinder is 3 cm.
The bowl of glass 3 is an inverted cone. The inside diameter is 6 cm and the inside slant height is 6 cm.
- Find the vertical height of the bowl of glass 3.
- Calculate the volume of the bowl of each of these glasses.
- Glass 2 is filled with water and then half the water is poured out. Find the height of the water.
[Adapted with permission from the Mathematics Assessment Project.]
IM Commentary
This task gives students an opportunity to work with volumes of cylinders, spheres and cones. Notice that the insight required increases as you move across the three glasses, from a simple application of the formula for the volume of a cylinder, to a situation requiring decomposition of the volume into two pieces, to one where a height must be calculated using the Pythagorean theorem.
The task can be used in the classroom to foster a number of discussions.
- First, although the task does not ask students to say which glass holds the most water and which holds the least, students could be asked to say what they think the answer is and then their estimates could be compared with the exact answers.
- Second, notice that the solution is framed in terms of knowing the volume for a cylinder or a cone in terms of the area of the base and the height, rather than formulas involving $r$ and $h$. This is intentional, since it allows for the observation that the volume of a cone is 1/3 the volume of a cylinder with the same base and height. The teacher could ask if this means that the volume of glass 3 is 1/3 the volume of glass 1. The answer is no, because glass 3 does not have height 6 cm, it has slant height 6 cm. This discussion could be used to highlight the need to attend to precision (in this case, the distinction between height and slant height).
- Finally, the question arises of whether answers should be given in exact form or as decimal approximations, and what are the advantages of each. Since the answers involve $\pi$ and square roots, decimal answers will necessarily be approximations; on the other hand, for practical purposes (e.g., how may glasses will you get out of a 1 liter bottle) a decimal approximation may be necessary.
Solution
The solutions use volume formulas for cylinders, cones and spheres. Note that all units are in terms of centimeters: area units are cm2, and volume units are cm3. The units are sometimes omitted for convenience. The diagrams are not to scale.
-
To find the vertical height of the bowl portion of the glass, we use the Pythagorean Theorem. $\text{Height in centimeters} = h=\sqrt{6^2 - 3^2}=\sqrt{36 - 9}=\sqrt{27}$. (Some may prefer to write $\sqrt{27}=3\sqrt3$.)

-
-
For glass 1 we use the fact that the volume of a cylinder is given by $V = (\text{area of base}) \cdot \text{height}$. Since the base is a circle with radius $r = \frac52$, the volume $V$ (in cm3) is $V= (\pi (\frac52)^2)\cdot6 = (\frac{75}{2}) \pi = 37 \frac12 \pi$.

-
For glass 2 the bowl consists of 2 parts- a cylinder of height and radius 3 which sits atop a hemisphere of radius 3. We add the volumes of these to get the total volume. For the cylinder portion, the volume (in cm3) is $(\pi 3^2)\cdot3=27 \pi$. For the volume of the hemisphere, take half the volume of a sphere of radius 3 to get: $\frac12 ( \frac43 \pi 3^3)= \frac12 (4\cdot 3^2 \pi) = 18 \pi$. Add these to get the total volume (in cm3): $27 \pi+18 \pi = 45 \pi$.

-
For the volume of the bowl of glass 3, use the fact that the volume of a cone is given by $V= \frac{1}{3} \text{Area of base}\cdot\text{Height}$. The radius is $3$ and the height is $\sqrt{27}$ by part (a). So the area of the base is $\frac13 \pi 3^2$ and the volume $V$ (in cm3 ) is $V= \frac13 \pi 3^2 \sqrt{27} = 3 \sqrt{27} \pi$. (Or $9 \sqrt{3} \pi$.)

-
-
Note first that the height of the liquid is measured from the bottom of the bowl of the glass.
The total volume of the glass is $45 \pi$, so if half the water is poured out then the remaining water occupies a volume of $\frac{45}{2} \pi$ , or $22 \frac12 \pi$. Notice that this is not just 3 cm up the glass since the hemispherical part of the glass holds less than the cylindrical part. (It is easy to see that if the glass had a cylindrical bottom, it would be bigger and so have a larger capacity.) As we saw in (b)(ii), the liquid in the glass fills the hemisphere first and then the cylindrical portion of the glass. The hemispherical part of the glass holds a volume of $18 \pi$, leaving a volume of $4 \frac12 \pi$, or $\frac92 \pi$, to fill the cylindrical portion.

The question is now reduced to finding the height of the liquid in the cylindrical portion of the glass. Once we know this height, we can simply add the height from the hemispherical portion, which is 3, and obtain the full height of the liquid in the glass.
To get the height of the liquid in the cylinder we compute the height of a cylinder which has volume $\frac92 \pi$. We use the formula for volume to solve for the height: $\frac92 \pi = \pi 3^2 h = 9\pi h$ so $h= \frac12$. We can now add 3 to this to get the required height of the liquid in the glass which is (in cm) $3 \frac12$.

Glasses
The diagram shows three glasses (not drawn to scale). The measurements are all in centimeters.

The bowl of glass 1 is cylindrical. The inside diameter is 5 cm and the inside height is 6 cm.
The bowl of glass 2 is composed of a hemisphere attached to cylinder. The inside diameter of both the hemisphere and the cylinder is 6 cm. The height of the cylinder is 3 cm.
The bowl of glass 3 is an inverted cone. The inside diameter is 6 cm and the inside slant height is 6 cm.
- Find the vertical height of the bowl of glass 3.
- Calculate the volume of the bowl of each of these glasses.
- Glass 2 is filled with water and then half the water is poured out. Find the height of the water.
[Adapted with permission from the Mathematics Assessment Project.]
