Laptop Battery Charge 2
Task
Jerry forgot to plug in his laptop before he went to bed. He wants to take the laptop to his friend's house with a full battery. The pictures below show screenshots of the battery charge indicator after he plugs in the computer.

- When can Jerry expect that his laptop battery is fully charged?
- At 9:27 AM Jerry makes a quick calculation:
The battery seems to be charging at a rate of 1 percentage point per minute. So the battery should be fully charged at 10:11 AM.
Explain Jerry's calculation. Is his estimate most likely an under- or over-estimate? How does it compare to your prediction? - Compare the average rate of change of the battery charging function on the first given time interval and on the last given time interval. What does this tell you about how the battery is charging?
- How long would it take for the battery to charge if it started out completely empty?
IM Commentary
This task uses a situation that is familiar to students to solve a problem they probably have all encountered before: How long will it take until an electronic device has a fully charged battery? A linear model can be used to solve this problem.
The task combines ideas from statistics, functions and modeling. It is a nice combination of ideas in different domains in the high school curriculum. Focus in high school means finding connections between the different topics that are covered. Lines of best fit are a perfect example of this idea since you are using linear functions to analyze data.
Students are not told how to come up with a model for the situation. Part of their job is to turn the screenshots into data that can be visualized with a scatter plot and analyzed with a linear function. A more scaffolded version of this task is shown for 8th grade: 8.SP.2 Laptop Battery Charge.
The task can be used for instruction with group work and whole class discussion. The last two parts of the task lead towards the question if a line is the best model for this situation. Close inspection shows that there seems to be some downward curvature to the data, which may agree with students' experiences when waiting for batteries to charge. On the other hand, while a line might not be the most accurate model, it is the simplest model that gives a result that is perfectly adequate for the situation, which is an important aspect of mathematical modeling.
The task provides good opportunities for students to engage in SMP 2 - Reason Abstractly and Quantitatively as well as SMP 4 - Model with Mathematics.
Solution
- In this situation we are looking at two variables: time, $t$ and battery charge, $b$. There are several ways we can choose units. A reasonable choice is "time in minutes since the laptop was plugged in" and "battery charge in percentage of full, %"
The laptop started charging at 9:11 a.m. and it was initially 41% charged. If we let $t$ be time since the laptop was plugged in, this information corresponds to the point with coordinates $(0,41).$ Similarly, we can translate the other screenshots into coordinate points: $(16, 56),\ (25, 64),\ (37, 74),\ (44, 79),\ (57, 86),\ (66, 91)$.
We can now make a scatter plot of the data to get an idea how the two variables are related.

It looks like there is a linear relationship between the variables.
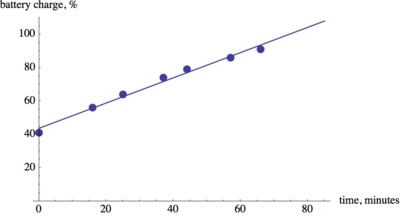
Using technology such as a graphing calculator or WolframAlpha we find that $b=43.7+0.757t.$
We can extend the line of best fit and see at what time it will reach an output value of 100%. This happens about 75 minutes after the computer was plugged in.
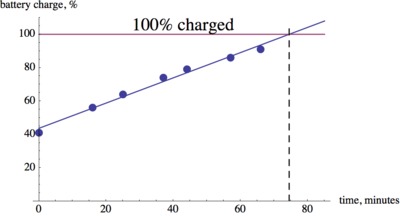
We can also use the equation to solve $b=43.7+0.757t=100$ for $t$ to obtain $t\approx 74.5$ minutes.
-
At 9:27 a.m. Jerry has two data points: $(0,41)$ and $(16,56)$. So the battery charged 15 percentage points in 16 minutes. That is almost 1 percentage point per minute. At 9:27 a.m. the battery still needs to charge 44 more percentage points, which will take approximately 44 minutes. So 44 minutes after 9:27 a.m. puts us at 10:11 a.m.
Jerry's estimate will probably be an underestimate for the time needed to fully charge the battery. He is overestimating the rate at which the battery is charging. Therefore, his calculation comes up with a shorter amount of time than is actually needed.
We can visualize Jerry's method with a line of slope 1 through the point $(16,56)$.

- The average rate of change of the battery charging function during the first time interval is $\displaystyle\frac{56-41}{16-0}=\frac{15}{16}=0.9375$ percentage points per minute. During the last time interval the average rate of change is $\displaystyle\frac{91 - 86}{66 - 57}=\frac{5}{9}\approx 0.556$ percentage points per minute. This means that as the battery gets charged, the rate at which it charges is going down. So it will take longer to go from 90% to 100% than it took to get from 40% to 50%.
-
We can use the line of best fit to find an estimate for the time it would take for the battery to charge from 0 to 100%. If we extend the line to the left, we see that it crosses the horizontal axis at about $-60$. So we can estimate that it would have taken 60 minutes for the battery to go from 0% to 41% and we already estimated that it would take about 75 minutes to go from 41% to 100%. So it would take about 135 minutes to charge the battery all the way from 0 to 100%.

This is probably not a bad estimate. Our average rate of change calculations show that we are probably underestimating the time it takes to charge the last 20 percentage points. But on the other hand, we probably overestimated the time it takes for the battery to go from 0 to 40%, so we should be close overall.
Laptop Battery Charge 2
Jerry forgot to plug in his laptop before he went to bed. He wants to take the laptop to his friend's house with a full battery. The pictures below show screenshots of the battery charge indicator after he plugs in the computer.

- When can Jerry expect that his laptop battery is fully charged?
- At 9:27 AM Jerry makes a quick calculation:
The battery seems to be charging at a rate of 1 percentage point per minute. So the battery should be fully charged at 10:11 AM.
Explain Jerry's calculation. Is his estimate most likely an under- or over-estimate? How does it compare to your prediction? - Compare the average rate of change of the battery charging function on the first given time interval and on the last given time interval. What does this tell you about how the battery is charging?
- How long would it take for the battery to charge if it started out completely empty?
