Use Cavalieri’s Principle to Compare Aquarium Volumes
Task
The management of an ocean life museum will choose to include either Aquarium A or Aquarium B in a new exhibit.
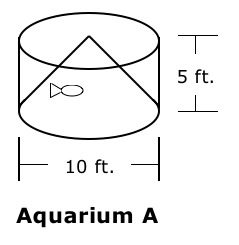
Aquarium A is a right cylinder with a diameter of 10 feet and a height of 5 feet. Covering the lower base of Aquarium A is an “underwater mountain” in the shape of a 5-foot-tall right cone. This aquarium would be built into a pillar in the center of the exhibit room.
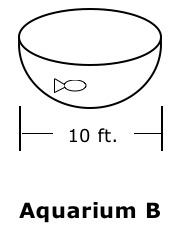
Aquarium B is half of a 10-foot-diameter sphere. This aquarium would protrude from the ceiling of the exhibit room.
How many cubic feet of water will Aquarium A hold?
For each aquarium, what is the area of the water’s surface when filled to a height of $h$ feet?
Use your results from parts (a) and (b) and Cavalieri's principle to find the volume of Aquarium B.
IM Commentary
This task presents a context that leads students toward discovery of the formula for calculating the volume of a sphere. Students who are given this task must be familiar with the formula for the volume of a cylinder, the formula for the volume of a cone, and Cavalieri’s principle.
Specific radius/diameter measurements help to make the procedure of analyzing cross-sections less daunting, but even so, finding expressions to represent areas of varying cross-sections is a very new and challenging skill for many students. For this reason, assigning this task within a setting where students can receive guidance from one another and from the instructor is a sensible alternative to using this task strictly as an assessment tool.
Submitted by Aaron Stidham to the Fourth illustrative Mathematics task writing contest.
Solution
-
The number of cubic feet of water that Aquarium A will hold is found by subtracting the volume of the cone from the volume of the cylinder:
$$ \text{Volume of Cylinder} - \text{Volume of Cone} = \text{Maximum Volume of Water for Aquarium A} $$ $$ \begin{align} \pi \times (\text{radius})^2 \times (\text{height}) - \frac13 \times \pi \times (\text{radius})^2 \times (\text{height}) &= \frac23 \times \pi \times (\text{radius})^2 \times (\text{height}) \\ &= \frac23 \times \pi \times 5^2 \times 5 \\ &= \frac{250\pi}{3} \approx 262 \end{align} $$ so Aquarium A can hold about 262 cubit feet of water. -
The area of the water’s surface at height $h$ can be derived by examining cross-sections. The radius and height of the cylinder and cone are both 5 feet, so the vertical cross-section through the vertex of the cone shown below shows that the cross section of the water forms an isosceles right triangle:

Therefore, the horizontal distance between the cone and the aquarium wall at height $h$ is also $h$.

The area of the water’s surface at height $h$ is found by subtracting the area of the inner circle, with radius $5 – h$, from the area of the outer circle, with radius 5.
$$ \text{Area of Outer Circle} - \text{Area of Inner Circle} = \text{Area of Water’s Surface at Height h} $$ $$ \begin{align} \pi \times 5^2 - \pi \times (5-h)^2 &= 25\pi - \pi (25-10h+h^2) \\ &= 25\pi - 25\pi + 10 \pi h - \pi h^2) \\ &= 10 \pi h - \pi h^2 \end{align} $$
When Aquarium A is filled to a height of $h$ feet, the area of the water’s surface is $10 \pi h - \pi h^2$ square feet.

Momentarily, the horizontal distance between the curved wall and the sphere’s center at height $h$ is denoted by $x$. But $x$ can be expressed in terms of $h$, since $x$ and $5 – h$ both represent leg lengths of a right triangle with hypotenuse 5: $$ \begin{align} x^2 + (5 – h)^2 &= 25 \\ x^2 + 25 – 10h + h^2 &= 25 \\ x^2 &= 10h – h^2 \\ x &= \sqrt{10h – h^2} \end{align} $$

In this case, the area of the water’s surface at height $h$ is simply the area of a circle whose radius is $\sqrt{10h – h^2}$: $$ \begin{align} \text{Area} &= \pi(\sqrt{10h – h^2})^2 \\ &= \pi(10h – h^2) \\ &= 10 \pi h - \pi h^2 \end{align} $$
Cavalieri’s principle states that two 3-dimensional solids of the same height are equal in volume if the areas of their horizontal cross-sections at every height $h$ are equal. Since both aquariums stand 5 feet tall, and since the area of the water’s surface when filled to a height of $h$ feet is the same for each aquarium, the volumes of water must be equal when both aquariums are filled to full capacity according to this principle. Therefore, no further calculations are necessary to determine that Aquarium B will hold $\frac{250 \pi }{3}\approx 262$ cubic feet of water, the very same volume that Aquarium A will hold.
Use Cavalieri’s Principle to Compare Aquarium Volumes
The management of an ocean life museum will choose to include either Aquarium A or Aquarium B in a new exhibit.
Aquarium A is a right cylinder with a diameter of 10 feet and a height of 5 feet. Covering the lower base of Aquarium A is an “underwater mountain” in the shape of a 5-foot-tall right cone. This aquarium would be built into a pillar in the center of the exhibit room.
Aquarium B is half of a 10-foot-diameter sphere. This aquarium would protrude from the ceiling of the exhibit room.


How many cubic feet of water will Aquarium A hold?
For each aquarium, what is the area of the water’s surface when filled to a height of $h$ feet?
Use your results from parts (a) and (b) and Cavalieri's principle to find the volume of Aquarium B.
