Ice Cream Cone
Task
You have been hired by the owner of a local ice cream parlor to assist in his company’s new venture. The company will soon sell its ice cream cones in the freezer section of local grocery stores. The manufacturing process requires that the ice cream cone be wrapped in a cone-shaped paper wrapper with a flat circular disc covering the top. The company wants to minimize the amount of paper that is wasted in the process of wrapping the cones. Use a real ice cream cone or the dimensions of a real ice cream cone to complete the following tasks.
- Sketch a wrapper like the one described above, using the actual size of your cone. Ignore any overlap required for assembly.
- Use your sketch to help you develop an equation the owner can use to calculate the surface area of a wrapper (including the lid) for another cone given its base had a radius of length, $r$, and a slant height, $s$.
- Using measurements of the radius of the base and slant height of your cone, and your equation from the previous step, find the surface area of your cone.
- The company has a large rectangular piece of paper that measures 100 cm by 150 cm. Estimate the maximum number of complete wrappers sized to fit your cone that could be cut from this one piece of paper. Explain your estimate.
IM Commentary
This rich task is an excellent example of geometric concepts in a modeling situation and is accessible to all students. In this task, students will provide a sketch of a paper ice cream cone wrapper, use the sketch to develop a formula for the surface area of the wrapper, and estimate the maximum number of wrappers that could be cut from a rectangular piece of paper. In the interest of modeling, no dimensions for the ice cream cone are given, though one particular set of such dimensions is assumed in several parts of the solutions below. The expectation is for students to use actual ice cream cones and a ruler or tape measure to determine the dimensions of their ice cream cone. In the event that this is not possible, one plausible alternative is to give the students an example of actual measurements similar to those used in the solutions provided. If access to the internet is available, another option is to allow students to research the possible dimensions of an ice cream cone.
This high demand task has a multitude of entry levels. Students will apply prior knowledge to solve this problem and their understanding of concepts such as areas of triangles, areas of rectangles, areas of circles, circumference, arc length, measures of a central angles, Pythagorean Theorem, metric conversion, and stacking methods will determine their entry level and solution path of choice. Many different solution paths are possible and should not be limited to the solutions provided. A list of suggested materials for this hands-on task is suggested.
Suggested Materials:
- Graph Paper
- Linear Measuring Tool
- Scissors
- Compass
- Protractor
- Tape
- Calculator
Solutions
Solution: Solution 1
Part (a) Basic Level Response
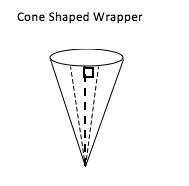
One approach is to sketch the conic template that is actually viewed in 3-dimensions as shown.
Sketch: Metric Units

Sketch: English Standard Units

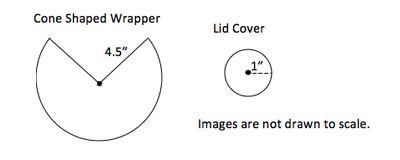
A second approach is to sketch the a 2-dimensional conic template as shown. This representation is evidence of residual knowledge.
Sketch: Metric Units

Sketch: English Standard Units
Solution: Solution 2
Part (a) Advanced Level Responses
The shapes drawn in the Basic Level Response representing the conic template is somewhat misleading when the actual dimensions are taken into account. Advanced students will identify the relationship between the circumference of the lid template and the arc length of the conic template. They may also determine the measure of the central angle defining the conic template is approximately 80°. The conic template will be drawn as shown.
Sketch: Metric Units

Sketch: English Standard Units

Solution: Solution 3
Part (b) Basic Level Responses
Develop Equation:
Students could divide the lateral surface of the cone into several triangles (with slightly curved bases) by extending line segments from the apex of the cone to the circular base of the cone. Using the area of a triangle formula and the circumference formula, students can determine a formula for the surface area of the cone.
Area of Triangle: $A = \frac12bh$
Circumference: $C = 2\pi r$

If we label the bases of the triangles by $b_1$, $b_2$, $b_3$, $b_4$, and so on, then the lateral surface area of the cone is the sum of the areas of the triangles:
$$\frac12 b_1 h + \frac12 b_2 h + \frac12 b_3 h + \frac12 b_4 h + \dots$$
Factoring out a $\frac{1}{2}h$ from each term, we find that the lateral surface area is given by the formula
$$
\frac{1}{2}h(\text{sum of the lengths of the bases)}.
$$
The sum of the lengths of the bases is (to a level of accuracy determined by how many triangles you take) just the circumference of the lid cover. Therefore, we conclude that $$
SA\text{(cone)} = \frac12 h (2\pi r)=\pi rh$$
Finally, we observe that the height $h$ of each triangle is precisely the slant height $s$ of the cone, so we can slightly re-write this formula as $SA\text{(cone)} = \pi rs$.
Since the area of the circular lid is given simply by $SA(\text{lid}) = \pi r^2$, the sum of these two formulas is the total surface area of wrapper required for a cone with length of radius of base $r$, and slant height $s$:
Total Surface Area (Cone and Circular Lid) $= \pi r s + \pi r^2$
Solution: Solution 4
Part (b) Advanced Level Response
Develop Equation:
Students create and solve a proportion comparing area to circumference. They use a circle containing the cone template and the circular lid. This method emphasizes an algebraic solution path.


$SA \text{(cone)} = \pi r s$
Area of the circular lid: $A = \pi r^2$
An equation the owner can use to calculate the surface area of a wrapper (including the lid) for another cone with length of radius of base $r$, and slant height $s$:
Total Surface Area (Cone and Circular Lid) $= \pi r s + \pi r^2$
Solution: Solution 5
Part (c) Solutions
Surface Area of Model: Metric Units
Students substitue their values into the formula.
$r = 2.5\text{ cm}$
$s = 11.5\text{ cm}$
$SA = \pi r s + \pi r^2$
$SA = \pi (2.5) (11.5) + \pi (2.5)^2$
$SA = 28.75 \pi + 6.25 \pi$
$SA = 35 \pi \approx 110\text{ cm}^2$
Surface Area of Model: English Standard Units
Students substitue their values into the formula.
$r = 1\text{ inch}$
$s = 4.5\text{ inches}$
$SA = \pi r s + \pi r^2$
$SA = \pi (1) (4.5) + \pi (1)^2$
$SA = 4.5 \pi + 1 \pi$
$SA = 5.5 \pi\approx 17\text{ in}^2$
Solution: Solution 6
Part (d) Basic Level Response
Maximum Number of Complete Wrappers cut from a 100 cm by 150 cm piece of paper
Metric Units
Students working with metric measurements throughout the solution path will not need to convert the dimensions of the paper. This is a stacking problem. Physical models of the templates for the complete wrapper and the rectangular piece of paper are helpful for students that tend to be visual learners. Some students may prefer to use graph paper to construct scale models. When available, drawing software can be useful and time saving.
Possible Misconceptions:
A common misconception is when students ignore the stacking component in this task. Some students simply divide the area of the paper by the area of one complete wrapper. This method does not account for the shapes of the conic wrapper or the circular lid cover. Using this method will yield an answer that is not realistic. An example of this is as follows.
Area of rectangular paper
$A = (\text{length})(\text{width})$
$A = (100)(150)$
$A = 15,000 \text{cm}^2$
$\frac{15000}{110}$ = $136$
Another flawed solution path results when students attempt to stack an incorrect representation of the conic template as shown previously in Part (a) Solution I (Basic Level Response).
Possible Solution Paths:
One solution path is to reshape the conic and circular wrapper so it will fit onto a rectangular template by doubling the length of the radius in each shape. Using the dimensions of the square templates, students will determine the number of squares that fit in the rectangular template. This method does not produce the maximum number and results in too much waste. Only 24 complete wrappers can fit onto the rectangular piece of paper using these dimensions. Metric units are used to model following the solution path.
$(2)(2.5 \text{ cm}) = 5 \text{ cm}$
$(2)(11.5 \text{ cm}) = 23 \text{ cm}$

An alternative solution path similar to the last method is to use an elongated rectangular conic template, rather than a square. The dimensions of the rectangle used will depend on the students approach. Some students may use the Pythagorean Theorem to approximate the length of the rectangle because an 80° angle is close to a 90° angle. In this case, the length of the rectangular template will be larger than needed and create additional wasted space when fitted onto the rectangular piece of paper. This method does not produce the maximum number and results in too much waste. Only 64 complete wrappers can fit onto the rectangular piece of paper using these dimensions. Metric units are used to model the following solution path.

Solution: Solution 7
Part (d) Advance Level Response
Maximum Number of Complete Wrappers cut from a 100 cm by 150 cm piece of paper
The following sketches show a high level of understanding with regard to stacking methods. The maximum number of complete ice cream cone wrappers using this method is approximately 110.
Students may elect to use slight variations of this method.


Ice Cream Cone
You have been hired by the owner of a local ice cream parlor to assist in his company’s new venture. The company will soon sell its ice cream cones in the freezer section of local grocery stores. The manufacturing process requires that the ice cream cone be wrapped in a cone-shaped paper wrapper with a flat circular disc covering the top. The company wants to minimize the amount of paper that is wasted in the process of wrapping the cones. Use a real ice cream cone or the dimensions of a real ice cream cone to complete the following tasks.
- Sketch a wrapper like the one described above, using the actual size of your cone. Ignore any overlap required for assembly.
- Use your sketch to help you develop an equation the owner can use to calculate the surface area of a wrapper (including the lid) for another cone given its base had a radius of length, $r$, and a slant height, $s$.
- Using measurements of the radius of the base and slant height of your cone, and your equation from the previous step, find the surface area of your cone.
- The company has a large rectangular piece of paper that measures 100 cm by 150 cm. Estimate the maximum number of complete wrappers sized to fit your cone that could be cut from this one piece of paper. Explain your estimate.
