Bicycle Wheel
Task
The wheels on a bicycle have a radius of 13 inches. One wheel is pictured below:

The point $O$ is the center of the wheel and a point $P$ on the circle is chosen. After the wheel has moved forward a distance of $d$, the point $P$ moves to a new point on the circle, marked $Q$ below:
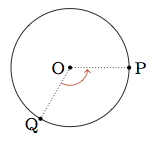
- Complete the table below, showing how the angle $QOP$ varies with the distance $d$ that the wheel has traveled forward:
Â
Angle measurements in degrees $d$ $m(\angle QOP)$ $\text{ in degrees}$ 1 inch  10 inches  3 feet  7 feet  - Recall that one radian is the measure of the angle cut out by a one unit length arc on a circle with radius one unit so $m(a) = 1$ radian in the picture below:
 More generally, a counterclockwise angle of $r$ radians is the angle cut out by an arc of length $r$ units on a unit circle. Â Using this definition of radian angle measure, complete the table below, showing how the angle $QOP$ varies with the distance $d$ that the wheel has traveled forward:
More generally, a counterclockwise angle of $r$ radians is the angle cut out by an arc of length $r$ units on a unit circle. Â Using this definition of radian angle measure, complete the table below, showing how the angle $QOP$ varies with the distance $d$ that the wheel has traveled forward:
Angle measurements in radians $d$ $m(\angle QOP)$ $\text{ in radians}$ 1 inch  10 inches  3 feet  7 feet  - What is the relationship between the measure of an angle in degrees and its measure in radians?
IM Commentary
The purpose of this task is to introduce radian measure for angles in a situation where it arises naturally. Radian measure focuses on the arc length of a circle cut out by a given angle. Degree measure, on the other hand, focuses on the angle. If the radius of the circle were one unit, then the radian measure table would be particularly simple to fill out. Even here where the radius is not one unit, the radian angle measure is more ''natural'' for this scenario because it measures the length of a circular arc and the distance a wheel is traveling is also the length of a circular arc. Â In the picture for part (b), we have assigned units of inches because these are the units used for measuring the bicycle wheel but inches could be replaced with any other unit of length.
The bike wheel can appear to spin in the clockwise or counterclockwise direction as the bike moves forward, depending on which side of the bike one is watching. Â For a clock too, if we are able to see the hands from behind the clock they too will appear to be moving in the counterclockwise direction. Â For this task, it has been assumed that the wheel is rotating in counterclockwise direction when the bike moves forward.
Students may already be familiar with the way to convert between degrees and radians: multiply by 360 and then divide by $2\pi$. In this case, they will be able to answer part (c) before completing the tables. The teacher may wish to focus on having students explain this conversion by looking at the number of degrees and radians in a full circle.
It is interesting to note that the picture of one radian gives us a good estimate, in degrees, for this angle: namely, if we replace the arc of the circle with a line segment of length one we would obtain an equilateral triangle and so an angle measure of 60. Â The curvature of the circle means that one radian measures a little less than 60 degrees.
Solution
-
One full revolution of the wheel would cover a distance equal to the wheel's circumference or $26\pi$ inches. We can set up a proportion to find out $m(\angle QOP)$, using the fact that there are 360$^\circ$ in a full circle. For example, going half a distance of half the circumference corresponds to $m(\angle QOP)=180^\circ$, half the total angle measure. More generally, traveling a distance of $d$ covers the corresponding proportion of angle measurement: We have $$ \frac{m(\angle QOP)}{360} = \frac{d}{26\pi} $$ Solving gives $m(\angle QOP) = \frac{360d}{26\pi}$, where $d$ is measured in inches.
Â
Angle measurements in degrees $d$ $m(\angle QOP)$ $\text{ in degrees}$ 1 inch $\frac{360}{26\pi}$ 10 inches $\frac{3600}{26\pi}$ 3 feet $\frac{360 \times 36}{26\pi}$ 7 feet $\frac{360 \times 84}{26\pi}$ -
Applying the given definition of a radian in the situation of the bike wheel, the radian measure of $\angle QOP$ is the length of the arc, on a unit circle, cut out by $\angle QOP$, as pictured below:

The arc is marked $d$ since this is the distance traveled by the bike as the wheel rotates and $P$ moves to $Q$. The bicycle wheel is a circle with a radius of 13 inches. Since all circles are similar, this means that if we divide the distance $d$ the wheel has traveled (in inches) by 13, this will give the length of the arc, on the unit circle, cut out by $\angle QOP$.
Â
Angle measurements in radians $d$ $m(\angle QOP)$ $\text{ in radians}$ 1 inch $\frac{1}{13}$ 10 inches $\frac{10}{13}$ 3 feet $\frac{36}{13}$ 7 feet $\frac{84}{13}$ - The angle measure in degrees is given by $\frac{360d}{26\pi}$ while its measure in radians is given by $\frac{d}{13}$. So to convert from radians to degrees we multiply by $\frac{360}{2\pi}$. To convert from degrees to radians we would mulitply by $\frac{2\pi}{360}$.
Bicycle Wheel
The wheels on a bicycle have a radius of 13 inches. One wheel is pictured below:

The point $O$ is the center of the wheel and a point $P$ on the circle is chosen. After the wheel has moved forward a distance of $d$, the point $P$ moves to a new point on the circle, marked $Q$ below:

- Complete the table below, showing how the angle $QOP$ varies with the distance $d$ that the wheel has traveled forward:
Â
Angle measurements in degrees $d$ $m(\angle QOP)$ $\text{ in degrees}$ 1 inch  10 inches  3 feet  7 feet  - Recall that one radian is the measure of the angle cut out by a one unit length arc on a circle with radius one unit so $m(a) = 1$ radian in the picture below:
 More generally, a counterclockwise angle of $r$ radians is the angle cut out by an arc of length $r$ units on a unit circle. Â Using this definition of radian angle measure, complete the table below, showing how the angle $QOP$ varies with the distance $d$ that the wheel has traveled forward:
More generally, a counterclockwise angle of $r$ radians is the angle cut out by an arc of length $r$ units on a unit circle. Â Using this definition of radian angle measure, complete the table below, showing how the angle $QOP$ varies with the distance $d$ that the wheel has traveled forward:
Angle measurements in radians $d$ $m(\angle QOP)$ $\text{ in radians}$ 1 inch  10 inches  3 feet  7 feet  - What is the relationship between the measure of an angle in degrees and its measure in radians?
