Satellite
Task
A satellite orbiting the earth uses radar to communicate with two control stations on the earth's surface. The satellite is in a geostationary orbit. That means that the satellite is always on the line through the center of the earth and control station 2.
From the perspective of Station 1, the satellite is on the horizon and from the perspective of station 2, the satellite is always directly overhead as in the following diagram. The angle between the lines from the satellite to the stations is $8.7^\circ$.
Assuming the Earth is a sphere with radius $3963$ miles, answer the following questions. Round all answers to the nearest whole number.
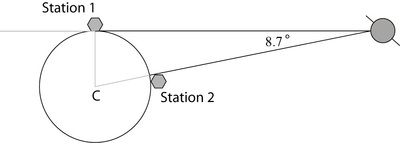
- How many miles will a signal sent from Station 1 to the satellite and then to Station 2 have to travel? Explain your answer.
- A satellite technician is flying from one station to the other in a direct path along the earth's surface. What is the distance she will have to fly? If she travels an average of 300 mph, how long will the trip take? Explain your answer.
- If a signal could travel through the earth's surface from one station to the other, what is the shortest distance the signal could travel to get from Station 1 to Station 2? Explain your answer.
IM Commentary
This task is an example of applying geometric methods to solve design problems and satisfy physical constraints. This task models a satellite orbiting the earth in communication with two control stations located miles apart on earths’ surface. Two given assumptions are the Earth is a sphere and the length of the radius of Earth is 3963 miles. Students are also provided with a diagram of the situation. Included in the diagram are line segments connecting the center of the Earth to each control station and connecting each control station to the satellite. The line segment connecting Station 1 to the satellite is drawn ‘on the horizon’ and is positioned tangent to the Earth. An angle measuring 8.7° is formed by line segments connecting the satellite to each control station. Students determine distances between various locations and given a rate of travel, students determine the time it takes to travel between two specified locations.
Students will apply prior knowledge to solve this problem and their understanding of concepts such as right triangle trigonometric functions, the perpendicular relationship associated with a radius of a circle drawn to a point of tangency, the Triangle Sum Theorem, and the Law of Cosines will lead them down well defined solution paths. The numbers used in this task are quite large, as they are representative of space travel. Encourage students to round solutions to the nearest whole number. A scientific or graphing calculator is needed to compute the values of trigonometric functions and square roots of large numbers.
Note:
With regard to part (a), it essential that students recognize the triangle formed in the diagram is a right triangle and justify this reasoning. Students should mention the perpendicular relationship between the radius drawn to Station 1 and the tangent line segment connecting Station 1 to the satellite. A reminder for students to verify their calculators are measuring in degrees and not in radians will eliminate possible measurement miscalculations.
With regard to part (b), it essential that students recognize the distance they are determining travels along the surface of the earth and is therefore not a linear path, but rather an arc length due to the spherical shape of the earth.
With regard to part (c), it essential that students recognize the triangle formed when connecting Station 1 to Station 2 to the center of the earth is not a right triangle.
Solutions
Solution: Solution 1
Part (a) Solution
Since the satellite is viewed on the horizon of Station 1, the line segment connecting Station 1 to the satellite is drawn tangent to the Earth. The point of tangency is located at Station 1.
The radius drawn to Station 1 (the point of tangency) is perpendicular to the line segment drawn tangent to the Earth, so the triangle formed by connecting the center of the Earth to Station 1 to the satellite is a right triangle.
- The hypotenuse of the right triangle is the line segment connecting the center of the Earth to the satellite because it is the side of the triangle that lies opposite the right angle located at the point of tangency (Station 1).
- The length of the shortest leg of the right triangle is the distance from the center of the Earth to Station 1, the given radius of 3,963 miles.
- The longest leg of the right triangle is the segment from Station 1 to the satellite.
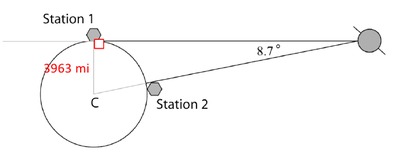
To solve for the distance the signal was sent, we must first calculate the length of the longest leg and the length of the hypotenuse as shown. Students may elect to use different trigonometric functions, because they are able to determine the measure of the third angle in the right triangle.
\begin{align} \tan{8.7} &= \frac{\text{length of shortest leg}}{\text{length of longest leg}} \cr \tan{8.7} &= \frac{\text{3963}}{\text{length of longest leg}} \cr \text{length of longest leg} &= \frac{3963}{\tan{8.7}} \cr\text{length of longest leg} &\approx 25,898 \end{align}Â
The distance from Station 1 to the satellite is approximately 25,898 miles. Similarly:
\begin{align} \sin{8.7} &= \frac{\text{length of shortest leg}}{\text{length of hypotenuse}} \cr \sin{8.7} &= \frac{\text{3963}}{\text{length of hypotenuse}} \cr \text{length of hypotenuse} &= \frac{3963}{\sin{8.7}} \cr \text{length of hypotenuse} &\approx 26,200 \end{align}Â
Thus the distance from the satellite to the center of the Earth is approximately 26,200 miles.
To determine the distance the signal was sent from Station 1 to the satellite to Station 2 we do not need the entire length of the hypotenuse, only the portion from the satellite to Station 2, so we must subtract the radius of the earth from the length of the hypotenuse:
$$26,200 – 3,963 = 22,237$$ In short:
Distance from Station 1 to satellite: 25,898 miles
Distance from satellite to Station 2: 22,237 miles
Total distance the signal was sent (the sum of these distances) is 48,135 miles.
Solution: Solution 2
Part (b) Solution
The distance the technician flies along the earth’s surface from Station 1 to Station 2 is not a linear path. The path of the plane is associated with arc length because the surface of the Earth is the surface of a sphere. To determine the distance the plane travels, we must solve for the length of an arc bounded by Station 1 and Station 2.
To use the arc length formula, it is necessary to first compute the measure of the angle formed by the two radii (central angle) in the right triangle. If the measure of an acute angle of a right triangle is equal to $8.7^{\circ}$, using the Triangle Sum Theorem, we can conclude the measure of the second acute angle must be equal to $81.3^{\circ}$.
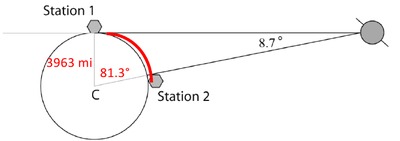
The distance the technician flies is now given by the length of this arc of the circle: $$ 3963\cdot 81.3^\circ\cdot\frac{\pi}{180^\circ}\approx 5,620\text{ miles.} $$
To find the time taken for this flight, we divide the distance just calculated by the rate of travel, assumed in the problem to be 300 mph: $$ \frac{5620}{300}\approx19\text{ hours.} $$
If the plane is traveling at a rate of 300 miles an hour, it will take the technician approximately 19 hours to travel from Station 1 to Station 2.
Solution: Solution 3
Part (c) Solution
Connecting Station 1 to Station 2 through the surface of earth forms a triangle that is not a right triangle as shown.
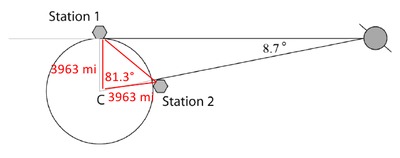
The Law of Cosines is used to determine the length of a side of a triangle when the lengths of two sides and measure of the included angle are known. This is our situation. Two sides of the triangle formed are radii of the earth (3963 miles) and the angle formed by the two radii measures $81.3^{\circ}$, as previously determined.
- Let $c$ represent the shortest distance between Station 1 and Station 2.
- Let $a$, and $b$ represent the lengths of the radii, 3963 miles.
- Let $81.3^{\circ}$ represent the measure of the included angle.
We solve for $c$ using the above values in the Law of Cosines: $$ c^2=3963^2+3963^2-2(3963)(3963)\cos(83.1^\circ)\approx 26,659,524. $$ Taking square roots, we find that the shortest distance the signal could travel through the earth’s surface from Station 1 to Station 2 is approximately 5,163 miles.
Satellite
A satellite orbiting the earth uses radar to communicate with two control stations on the earth's surface. The satellite is in a geostationary orbit. That means that the satellite is always on the line through the center of the earth and control station 2.
From the perspective of Station 1, the satellite is on the horizon and from the perspective of station 2, the satellite is always directly overhead as in the following diagram. The angle between the lines from the satellite to the stations is $8.7^\circ$.
Assuming the Earth is a sphere with radius $3963$ miles, answer the following questions. Round all answers to the nearest whole number.

- How many miles will a signal sent from Station 1 to the satellite and then to Station 2 have to travel? Explain your answer.
- A satellite technician is flying from one station to the other in a direct path along the earth's surface. What is the distance she will have to fly? If she travels an average of 300 mph, how long will the trip take? Explain your answer.
- If a signal could travel through the earth's surface from one station to the other, what is the shortest distance the signal could travel to get from Station 1 to Station 2? Explain your answer.
