Task
Cruz and Erica were both getting ready for soccer.
Erica said,
I ran more laps, so I ran farther.
Cruz said,
4 laps around the school is 1 mile, but it takes 12 laps around the playground to go 1 mile. My laps are much longer, so I ran farther.
Who is right? Draw a picture to help you explain your answer.
IM Commentary
The purpose of this task is for students to compare two fractions that arise in a context. Because the fractions are equal, students need to be able to explain how they know that. Some students might stop at the second-to-last picture and note that it looks like they ran the same distance, but the explanation is not yet complete at that point. Just because to pictures look the same doesn't mean they are. Think of a picture representing $\frac{49}{100}$ and $\frac{50}{99}$--these will look very similar, but they are not, in fact, equal. To explain why Erica and Cruz ran the same distance, we have to explain why $\frac14 = \frac{3}{12}$.
Note that this task illustrates the cluster "4.NF.A Extend understanding of fraction equivalence and ordering" because it addresses elements of both the standards within this cluster.
Solution
Let’s begin with a picture representing $1$ mile.

With this picture in mind, we can see that one lap around the school is $\frac14$ mile:

and we can see that one lap around the playground is $\frac{1}{12}$ mile:
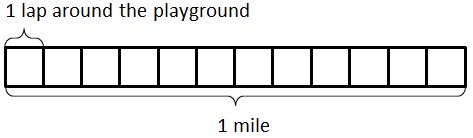
Since Erica ran 3 laps around the playground, she ran $\frac{3}{12}$ mile. Since Cruz ran 1 lap around the school, he ran $\frac14$ mile:
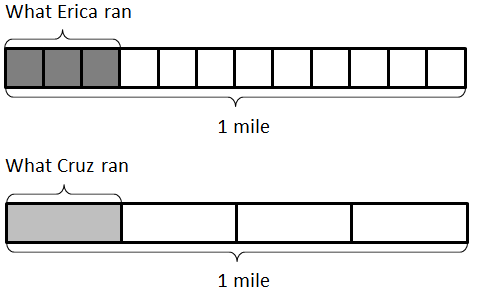
Now looking at the pictures above, it looks like they actually ran the same distance. We can show this is true if we divide each of the laps around the school into three equal pieces:
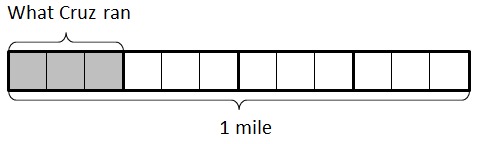
When we subdivide each $\frac14$ mile lap into three equal pieces, our mile is divided into 12 equal pieces. The piece that represents Cruz's run is now divided into 3 pieces, and so $\frac14 = \frac{3}{12}$ he ran the same distance that Erica ran.





