Identifying Multiples

Task

Below is a multiplication table for single digit numbers:

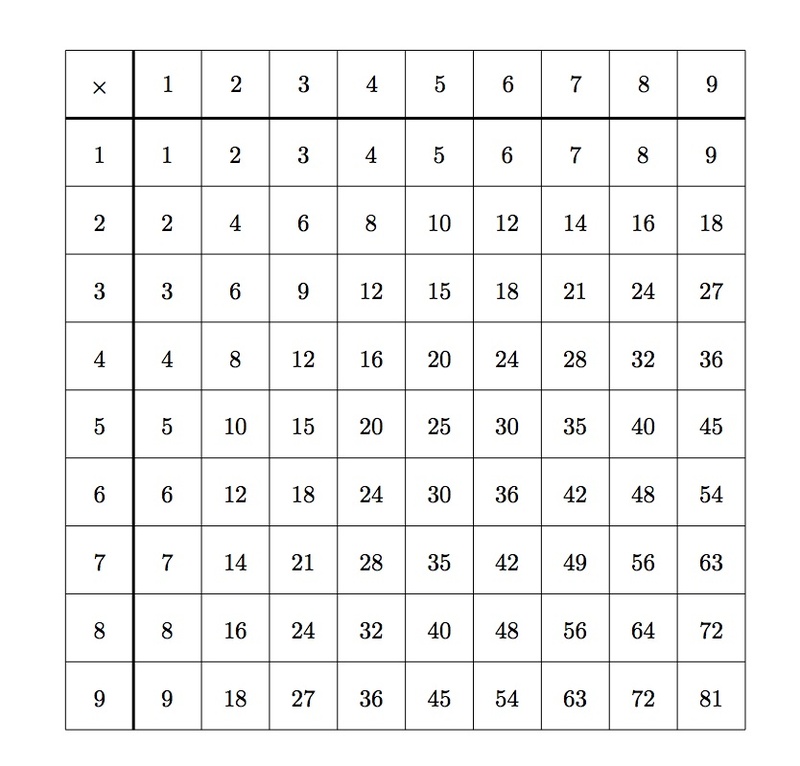
Use a different copy of the multiplication table for each of the questions below:

1. Color all boxes with multiples of 2 in the multiplication table. What pattern do you see in the colored boxes?
2. Color all boxes with multiples of 3 in the table. How does the pattern of multiples of 3 compare to the pattern of multiples of 2?
3. Color all boxes with multiples of 4 in the table. How is this different from the patterns in (a) and (b)? Why?

IM Commentary

The goal of this task is to work on finding multiples of some whole numbers. After shading in the multiples of 2, 3, and 4 on the table, students will see a key difference. For the multiples of 2, every second column and every second row is shaded. Similarly for the multiples of 3 every third column and every third row is shaded. For the multiples of 4, every fourth column and every fourth row is shaded. But, unlike for multiples of 2 and 3, there are also several isolated boxes that are multiples of 4.

The reason for this is that 2 and 3 are prime, but 4 is composite. A composite number can be written as a product of two smaller whole numbers, but a prime number cannot. In terms of the pictures, consider the isolated box $2 \times 6 = 12$ in the table of multiples of 4. This isolated box occurs because 2 is a factor of 6, and it combines with the other two to make a multiple of 4:

So it is possible to create a multiple of 4 without multiplying 4 by another number. With primes like 2 and 3, this is not possible.

In the fourth grade, the emphasis here should be on seeing that there is a visual difference in patterns and that this difference is related to whether and how numbers factor. This task could be used to introduce the notion of a prime number, or if students are already familiar with primes and composites, this is a good task to reinforce these ideas.

Solution

1. The even numbers are shaded blue in the table below while the odd numbers in the table are left white:

   

   Every other row (the even numbered rows) is filled with even numbers and similarly every other column (the even numbered columns) is filled with even numbers. The reason for this pattern is that a product $a \times b$ is even when at least one of its factors, $a$ or $b$, is even.

2. The multiples of three are shaded blue in the table below while the other numbers in the table are left white:

   

   Every third row is filled with multiples of three and similarly every third column is filled with multiples of three. The reason for this pattern is that a product $a \times b$ is divisible by three when at least one of $a$ or $b$ is divisible by three.

3. The multiples of four are shaded blue in the table below while the other numbers in the table are left white:

   

   There is a clear difference between the pattern of multiples of $4$ and those of $2$ and $3$ seen above in parts (a) and (b). As in parts (a) and (b), every fourth column and every fourth row is shaded as these are multiples of $4$. There are, however, additional isolated shaded boxes. One of these is $2 \times 2 = 4$. The reason why these isolated boxes occur for multiples of $4$ while they did not occur for multiples of $2$ or $3$ is that $4$ can be written as a product of smaller positive whole numbers ($2 \times 2$). So for example in the box $6 \times 6$, each factor of $6$ is divisble by $2$ and so the product $6 \times 6$ is divisible by $4$ (even though neither factor of $6$ is divisible by $4$). Since $2$ and $3$ are prime numbers they cannot be written as a product of smaller whole numbers and so these isolated shaded boxes do not occur for multiples of $2$ and $3$.