Scaling Up and Down
Alignments to Content Standards:
5.NF.B.5
Task
The fifth grade teachers are in charge of planning the annual Davis Elementary Fun Run. The teachers decide that each adult should run $\frac{6}{4}$ as far as each student in grade 5 and each student in grade 1 should run $\frac{3}{4}$ as far as each student in grade 5.
-
Who has to run the longest distance? Who has to run the shortest distance? Explain your reasoning.
-
The fifth grade students decide that they should each run four laps around the track. How many laps should each adult and each first grade student run?
-
Peyton, a fifth grader calculates that he will run a$\frac{1}{2}$ mile. Write two multiplication equations involving $\frac{1}{2}$, one that shows how many miles each adult will run and one that shows how many miles each first grade student will run.
-
When Peyton showed the adults his calculations, some of them were confused. Some of the adults thought multiplication always makes a number larger, for example $2\times5$ is bigger than 5. When calculating the distance the first graders ran, Peyton used multiplication but got a smaller number. Explain why the product of 5 and another number is not always greater than 5, and write an example to help the adults understand.
-
Presley, another fifth grade student, wanted to write the distance she ran in eighths. She noticed that you could write this equation: $\frac{4}{4}\times\frac{1}{2}$miles = $\frac{4}{8}$ miles. Explain why in this case multiplying by $\frac{1}{2}$ results in a product that is neither larger nor smaller than $\frac{1}{2}$.
IM Commentary
This task is structured so that a teacher can diagnose the depth of a student’s understanding of what it means to multiply a number by a fraction, specifically in terms of scaling (as such it can be used formatively or summatively). Part A addresses whether or not a student understands basic fraction comparisons, and helps set them up to reason about the subsequent problems. Part B assesses whether students can recognize a context in which scaling is appropriate, and then assesses whether or not they can multiply a whole number by a fraction (both larger and smaller than 1). Part C looks at whether students can extend their knowledge of scaling to when both factors are fractions (the first situation has one number smaller and one number greater than 1, and in the second both are smaller than one). Part D asks students to justify an argument about multiplication, and Part E connects fraction equivalence with the effect of multiplying a number by 1.
This task was written as part of a collaborative project between Illustrative Mathematics, the Smarter Balanced Assessment Consortia, and the Teaching Channel.
Solution
- The adults will run the farthest, and the first grade students will run the shortest distance. Reasoning could include:
-
Pictures or comments directly comparing $\frac64$ with $\frac34$ (e.g. one is greater than a whole and the other is less)
-
Commentary that $\frac64$ is double $\frac34$ because the denominators are the same but the numerator is twice as large.
-
Commentary that since $\frac64 = \frac32$, it is therefore double $\frac34$ because the numerators are equal but the denominator is half.
-
$\frac64 \times 4 = 6$ laps for the adults.
$\frac34 \times 4 = 3$ laps for the first grade students.
In this assessment task, students are not required to use a diagram, although of course they may. For this part, a diagram could look like either of the ones below

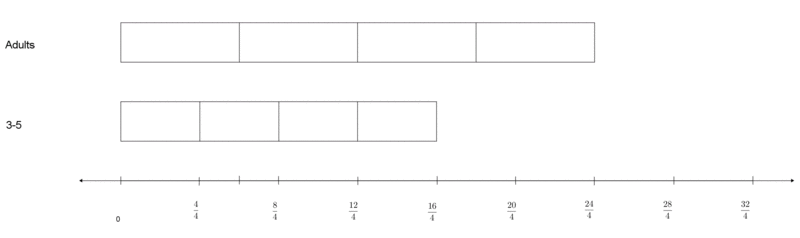
In the first picture, the student shows the grades 3-5 students run 4 laps, and subdivides that into four equal groups. He or she then reasons that the adults must run $\frac64$ that number and the K-2 students must run $\frac34$ that number. In the second picture, the student is showing that for each lap the 3-5 students run, the adults must run $\frac64$ of a lap. Therefore, since the 3-5 students run four laps (or $\frac{16}{4}$ laps), the adults must run a total of six ($\frac{24}{4}$) laps.
-
$\frac64 \times \frac12 = \frac68$ or $\frac34$ miles for the adults.
$\frac34 \times \frac12 = \frac38$ miles for the K-2 students.
For Part C, a student may create a representation for adults as below:
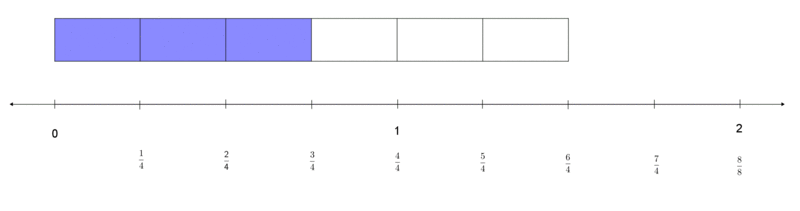
-
If you multiply 5 by a number greater than 1, then the product will be greater than 5. If you multiply 5 by a number less than 1, then the product will be less than 5. For example, $\frac{1}{10} \times 5 = \frac12$.
-
In this example, you are multiplying by a fraction equivalent to 1. When you multiply a number by 1, you get the same number (or a number that is equivalent). When you multiply a number by a number less than 1, you get a smaller product. When you multiply a number by a number greater than 1, you get a larger product.



