Sidewalk Patterns
Task
Cora and Cecilia each use chalk to make their own number patterns on the sidewalk. They make each of their patterns 10 boxes long and line their patterns up so they are next to each other.
Cora puts 0 in her first box and decides that she will add 3 every time to get the next number.
Cecilia puts 0 in her first box and decides that she will add 9 every time to get the next number.

- Complete each girl's sidewalk pattern.
- How many times greater is Cecilia’s number in the 5th box be than Cora’s number in the 5th box? What about the numbers in the 8th box? The 10th box?
- What pattern do you notice in your answers for part b? Why do you think that pattern exists?
- If Cora and Cecilia kept their sidewalk patterns going, what number will be in Cora's box when Cecilia's corresponding box shows 153?
IM Commentary
This purpose of this task is to help students articulate mathematical descriptions of number patterns. Though Cora and Cecilia's patterns are separate, we notice an interesting relationship emerge between corresponding terms in their patterns. For any given term, we will notice that Cecilia's number will always be three times Cora's number. Students may also notice that if we kept both patterns going indefinitely, Cecilia's numbers would always show up in Cora's path, though only some of Cora's numbers will show up in Cecilia's path.
The Standards for Mathematical Practice focus on the nature of the learning experiences by attending to the thinking processes and habits of mind that students need to develop in order to attain a deep and flexible understanding of mathematics. Certain tasks lend themselves to the demonstration of specific practices by students. The practices that are observable during exploration of a task depend on how instruction unfolds in the classroom. While it is possible that tasks may be connected to several practices, only one practice connection will be discussed in depth. Possible secondary practice connections may be discussed but not in the same degree of detail.
This task helps illustrate Mathematical Practice 8, Look for and express regularity in repeated reasoning. During this activity, fifth graders are actively comparing Celia’s and Cora’s sidewalk patterns and noticing any connections between the two. They are asked to directly compare numbers generated from a repeated pattern in certain boxes in order to draw conclusions and generalize a pattern between the sets of numbers. This explanation of “Why?” draws upon MP.3, Construct viable arguments and critique the reasoning of others. Through this in-depth exploration of these two sidewalk patterns, students are immersed in pattern-recognition and pattern-generalizing which not only develops a better understanding of how numbers behave in our base ten system, but pushes students to generalize by reasoning repeatedly. Students will notice that Celia’s numbers will always appear in Cora’s numbers but the opposite isn’t true. Then they will observe that Cecilia’s terms are always three times Cora’s corresponding term. A full explanation of this thinking is detailed in the solution set. While looking closely at the repeated pattern and making generalizations students are also engaged in examining the structure of the number sets and making use of that structure in their comparisons (MP.7).
Solutions
Solution: 1
a.
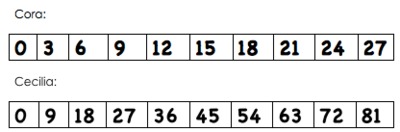
b.
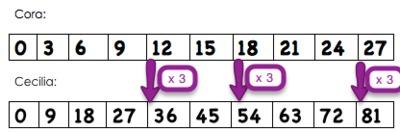
We can see that at the 5th, 8th and 10th boxes, Cecilia's number is always 3 times Cora's number.
Cecilia's number will always be three times Cora's number, no matter which pair of corresponding boxes the girls stand on. Cora's box shows 0 and the multiples of 3. Cecilia's box shows 0 and the multiples of 9.
c.

The image above shows us the 3 as a factor in each of Cora's terms in her path. It also shows the 9 as a factor in each of Cecilia's terms in her path, though 9 is being represented as 3 x 3. This allows us to see that Cora's factor of 3 is contained in each of Cecilia's terms, as well as one extra factor of 3. This is why Cecilia's term will always be three times Cora's corresponding term in her path.
d.
If Cecilia's box shows 153, then Cora's corresponding box must have 51. We know that Cecilia's box will always show three times as much as Cora's corresponding box, so Cora's box must show 51.
Solution:
Sidewalk Patterns
Cora and Cecilia each use chalk to make their own number patterns on the sidewalk. They make each of their patterns 10 boxes long and line their patterns up so they are next to each other.
Cora puts 0 in her first box and decides that she will add 3 every time to get the next number.
Cecilia puts 0 in her first box and decides that she will add 9 every time to get the next number.

- Complete each girl's sidewalk pattern.
- How many times greater is Cecilia’s number in the 5th box be than Cora’s number in the 5th box? What about the numbers in the 8th box? The 10th box?
- What pattern do you notice in your answers for part b? Why do you think that pattern exists?
- If Cora and Cecilia kept their sidewalk patterns going, what number will be in Cora's box when Cecilia's corresponding box shows 153?
