Riding by the Library
Task
Nina rides her bike from her home to school passing by the library on the way, and traveling at a constant speed for the entire trip. (See map below.)

- Sketch a graph of Nina’s distance from school as a function of time.
- Sketch a graph of Nina’s distance from the library as a function of time.
IM Commentary
In this task students draw the graphs of two functions from verbal descriptions. Both functions describe the same situation but changing the viewpoint of the observer changes where the function has output value zero. This small twist forces the students to think carefully about the interpretation of the dependent variable. This task could be used in different ways:
- To generate a class discussion about graphing.
- As a quick assessment about graphing, for example during a class warm-up.
- To engage students in small group discussion.
There are several extension possible for this task. For example: The assumption that Nina rides at a constant speed for the entire trip is not really realistic. At the very least, she has to speed up at the beginning and slow down when she gets to school. How does this change the graph?
Solution
-
We can describe the important features of the graph:
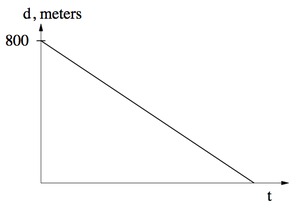
- Nina’s distance function from school starts with the largest output value at $t = 0$ when she starts her ride to school.
- When Nina arrives at school, her distance from school is 0 and the ride is over. Therefore, the last point on the graph is on the $t$-axis.
- Nina’s speed is constant throughout her ride, so the graph is a line with negative slope.
- In this problem we don’t know how long it takes Nina to ride to school. We only know the distance she is riding. We can label the vertical intercept because we know that Nina’s home is 800 meters from her school.
In this case the situation has not changed, we still have to sketch a distance graph, but the distance is now measures from the library and not from home. We can imagine a person standing at the library watching Nina’s ride. Again, we can describe the important features of the graph:
- The initial distance from the library is 200 meters.
- The distance decreases until it reaches 0 meters when Nina arrives at the library.
- The distance from the library then increases and reaches its maximum when Nina arrives at school.
- The absolute values of the slopes of the two lines are equal since Nina rides at a constant speed.
- We can label the function values of the starting and ending points of the graph with 200 meters and 600 meters, respectively.

Riding by the Library
Nina rides her bike from her home to school passing by the library on the way, and traveling at a constant speed for the entire trip. (See map below.)

- Sketch a graph of Nina’s distance from school as a function of time.
- Sketch a graph of Nina’s distance from the library as a function of time.
