Writing constraints
Task
In (a)–(d), (i) write a constraint equation, (ii) determine two solutions, and (iii) graph the equation and mark your solutions.
- The relation between quantity of chicken and quantity of steak if chicken costs \$1.29/lb and steak costs \$3.49/lb, and you have \$100 to spend on a barbecue.
- The relation between the time spent walking and driving if you walk at 3 mph then hitch a ride in a car traveling at 75 mph, covering a total distance of 60 miles.
- The relation between the volume of titanium and iron in a bicycle weighing 5 kg, if titanium has a density of 4.5g/cm${}^3$ and iron has a density of 7.87 g/cm${}^3$ (ignore other materials).
- The relation between the time spent walking and the time spent canoeing on a 30 mile trip if you walk at 4 mph and canoe at 7 mph.
IM Commentary
The purpose of this task is to give students practice writing a constraint equation for a given context. Instruction accompanying this task should introduce the notion of a constraint equation as an equation governing the possible values of the variables in question (i.e., "constraining" said values). In particular, it is worth differentiating the role of constraint equations from more functional equations, e.g., formulas to convert from degrees Celsius to degree Fahrenheit. The task has students interpret the context and choose variables to represent the quantities, which are governed by the constraint equation and the fact that they are non-negative (allowing us to restrict the graphs to points in the first quadrant only).
The four parts are independent and can be used as separate tasks.
This task is adapted from Algebra: Form and Function, McCallum et al., Wiley 2010.
Solution
-
- Let $c$ be the number of pounds of chicken you buy and $s$ the number of pounds of steak. Then $1.29c + 3.49s = 100$.
- Many combinations are reasonable. For example, you could buy 10 lbs of chicken, so that $c = 10$. This gives
\begin{eqnarray*} 1.29 \cdot 10 + 3.49 s &=& 100 \cr s &=& (100 - 12.9)/3.49\cr &=& 24.957 \\ &\approx& 25.0. \end{eqnarray*}So you would buy approximately 25 lb of steak. Thus $(10,25)$ is one reasonable solution. Alternatively, you could buy 25 lb of chicken, so that $c = 25$, and compute:\begin{eqnarray*} 1.29 \cdot 25 + 3.49 s &=& 100 \cr s &=& (100 - 1.29 \cdot 25)/3.49\cr &=& 19.412\cr &\approx& 19.4. \end{eqnarray*}So you would buy about 19.4 lb of steak. Thus $(25, 19.4)$ is another reasonable solution.

-
- If you walk for $w$ hours and drive for $d$ hours, then $3w + 75d = 60$.
- If you walk for 2 hours, then $w = 2$,
\begin{eqnarray*} 3 \cdot 2 + 75 d &=& 60 \\ d &=& (60 - 6)/75 = 0.72, \end{eqnarray*}so you ride for 0.72 hours, or $0.72 \cdot 60 \approx 43$ minutes. So $(2,0.72)$ is one reasonable solution. If you walk for 5 hours, then $w = 5$, so\begin{eqnarray*} 3 \cdot 5 + 75 d &=& 60 \\ d &=& (60 - 15)/75 = 0.6, \end{eqnarray*}so you ride for 0.6 hours, or $0.6 \cdot 60 = 36$ minutes. So another reasonable solution is $(5, 0.6)$.

-
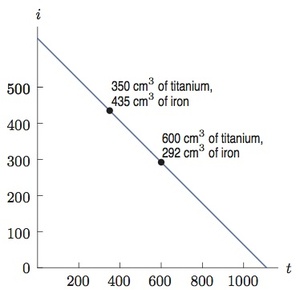
- If $t$ is the volume of titanium and $i$ is the volume of iron (in cm$^3$), then $4.5 t + 7.87 i = 5000$. Note that the density is given in grams and the total weight of the bicycle is given in kg, so we must convert 5 kg to 5000 g.
- If you use 600 cm${}^3$ of titanium, then $t = 600$, and
\begin{eqnarray*} 4.5\cdot 600 + 7.87 i &=& 5000 \\ i &=& (5000 - 4.5 \cdot 600)/7.87 = 292.25, \end{eqnarray*}so you would use about 292 cm$^3$ of iron. So a possible solution is $(600, 292)$. Or you could use 350 cm$^3$ of titanium, so\begin{eqnarray*} 4.5\cdot 350 + 7.87 i &=& 5000 \\ i &=& (5000 - 4.5 \cdot 350)/7.87 = 435.20, \end{eqnarray*}so you would use about 435 cm$^3$ of iron. So a possible solution is $(350, 435)$.
-
- If $w$ is the time spent walking and $c$ is the time spent canoeing, both in hours, then $4w + 7c = 30$.
- If you walk for 3 hours then $w = 3$, so
\begin{eqnarray*} 4 \cdot 3 + 7 c &=& 30\\ c &=& (30 - 12)/7 = 2.57, \end{eqnarray*}so you canoe for about 2.6 hours. So one possible solution is $(3, 2.6)$. If you walk for 1 hour, then $w = 1$, so\begin{eqnarray*} 4 \cdot 1 + 7 c &=& 30\\ c &=& (30 - 4)/7 = 3.71, \end{eqnarray*}so you canoe for about 3.7 hours. So another possible solution is $(1, 3.7)$.

Writing constraints
In (a)–(d), (i) write a constraint equation, (ii) determine two solutions, and (iii) graph the equation and mark your solutions.
- The relation between quantity of chicken and quantity of steak if chicken costs \$1.29/lb and steak costs \$3.49/lb, and you have \$100 to spend on a barbecue.
- The relation between the time spent walking and driving if you walk at 3 mph then hitch a ride in a car traveling at 75 mph, covering a total distance of 60 miles.
- The relation between the volume of titanium and iron in a bicycle weighing 5 kg, if titanium has a density of 4.5g/cm${}^3$ and iron has a density of 7.87 g/cm${}^3$ (ignore other materials).
- The relation between the time spent walking and the time spent canoeing on a 30 mile trip if you walk at 4 mph and canoe at 7 mph.
