Task
Enrico has discovered a geometric technique for ''completing the square'' to find the solutions of quadratic equations. To solve the equation $x^2 + 6x + 4 = 0$, Enrico draws a square of dimension $x$ by $x$ and attaches 6 strips (3 of dimension 1 by $x$ and 3 of dimension $x$ by 1) to make the picture below:
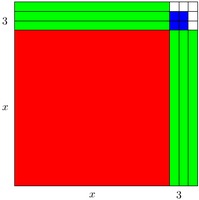
To complete the larger square, Enrico adds 9 squares of dimension 1 by 1. He has 4 of them in his initial expression so he needs five more as shown in the picture. So the picture represents the equation $$ (x+3)^2 = (x^2 + 6x + 4) + 5 $$
- Explain how Enrico's method helps find the roots of $x^2 + 6x + 4 = 0$.
- Help Enrico draw a picture for, and then solve, the equation $x^2 - 6x + 4 = 0$.
IM Commentary
The purpose of this task is to help provide geometric intuition for the algebraic process called ''completing the square.'' This is often done to help solve quadratic equations but the reason why the process is called completing the square is usually not highlighted. It turns out that when the algebraic expressions are modeled geometrically we find part of a square which is missing a small piece in order to be complete. For the two quadratic equations considered here, the roots are real. This process applies to all quadratic equations, however, and is one of the best known methods for deriving the quadratic formula. If students are comfortable with the examples given here, the teacher might want to explore what happens when the coefficients of the quadratic equation are variables (and hence work toward deriving the quadratic formula).


