Solution Sets
Task
Given below are the graphs of two lines, $y=-0.5 x + 5\ $ and $y=-1.25 x + 8,$ and several regions and points are shown. Note that $C$ is the region that appears completely white in the graph.
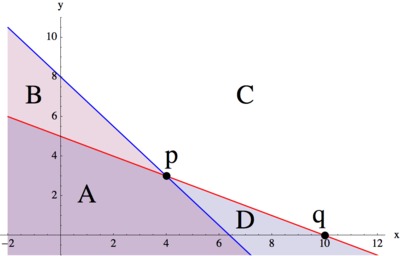
- For each region and each point, write a system of equations or inequalities, using the given two lines, that has the region or point as its solution set and explain the choice of $\leq,\, \geq$, or $=$ in each case. (You may assume that the line is part of each region.)
- The coordinates of a point within a region have to satisfy the corresponding system of inequalities. Verify this by picking a specific point in each region and showing that the coordinates of this point satisfy the corresponding system of inequalities for that region.
- In the previous part, we checked that specific coordinate points satisfied our inequalities for each region. Without picking any specific numbers, use the same idea to explain how you know that all points in the 3rd quadrant must satisfy the inequalities for region A.
IM Commentary
The typical system of equations or inequalities problem gives the system and asks for the graph of the solution. This task turns the problem around. It gives a solution set and asks for the system that corresponds to it. The purpose of this task is to give students a chance to go beyond the typical problem and make the connections between points in the coordinate plane and solutions to inequalities and equations. Students have to focus on what the graph is showing. When you are describing a region, why does the inequality have to go one way or another? When you pick a point that clearly lies in a region, what has to be true about its coordinates so that it satisfies the associated system of inequalities?
The last part of this problem requires the students to make a general argument without using specific numbers (SMP 4) and instead to recognize the structure of the inequalities (SMP 7).
The task could be used in many instructional settings, but having students share their thinking and respond to each others' arguments would provide a rich learning experience.
Solution
The blue line has equation $y=−1.25x+8$ and the red line has equation $y=−0.5x+5.$
- Region A: Since any point in region A lies on or below the red line and on or below the blue line, it has to be true that the point's $y$-coordinate has to be less than or equal to $−1.25x+8$ and less than or equal to $−0.5x+5.$ Therefore, the system of inequalities which describes region A is: \begin{eqnarray*} y&\leq&-0.5 x + 5\\ y&\leq&-1.25 x + 8 \end{eqnarray*} Region B: Since any point in region B lies on or below the blue line and on or above the red line, it has to be true that the point's $y$-coordinate has to be less than or equal to $−1.25x+8$ and greater than or equal to $−0.5x+5.$ Therefore, the system of inequalities which describes region B is: \begin{eqnarray*} y&\geq&-0.5 x + 5\\ y&\leq&-1.25 x + 8 \end{eqnarray*} Region C: Since any point in region C lies on or above the red line and on or above the blue line, it has to be true that the point's $y$-coordinate has to be greater than or equal to $−1.25x+8$ and greater than or equal to $−0.5x+5.$ Therefore, the system of inequalities which describes region C is: \begin{eqnarray*} y&\geq&-0.5 x + 5\\ y&\geq&-1.25 x + 8 \end{eqnarray*} Region D: Since any point in region D lies on or below the red line and on or above the blue line, it has to be true that the point's $y$-coordinate has to be greater than or equal to $−1.25x+8$ and less than or equal to $−0.5x+5.$ Therefore, the system of inequalities which describes region D is: \begin{eqnarray*} y&\leq&-0.5 x + 5\\ y&\geq&-1.25 x + 8 \end{eqnarray*} Point p: Since point p lies on the red line and also lies on the blue line, it has to be true that p's $y$-coordinate is equal to both $−1.25x+8$ and to $−0.5x+5.$ Therefore, the system of equations which describes point p is: \begin{eqnarray*} y&=&-0.5 x + 5\\ y&=&-1.25 x + 8 \end{eqnarray*} Point q: Since point q lies on the red line and also lies on $x$-axis, it has to be true that q's $y$-coordinate is equal to both $−1.25x+8$ and to $0.$ Therefore, the system of equations which describes point q is: \begin{eqnarray*} y&=&0\\ y&=&-0.5 x + 5\\ \end{eqnarray*}
-
Many answers are possible. We give one for each region.
The point $(0,0)$ lies in region A: Substituting this point into the inequalities we have \begin{eqnarray*} 0&\leq&-0.5\cdot 0 + 5=5\\ 0&\leq&-1.25\cdot 0 + 8=8, \end{eqnarray*} which is true.
The point $(0,6)$ lies in region B: Substituting this point into the inequalities we have \begin{eqnarray*} 6&\geq&-0.5\cdot 0 + 5 = 5\\ 6&\leq&-1.25\cdot 0 + 8 = 8, \end{eqnarray*} which is true.
The point $(8,10)$ lies in region C: Substituting this point into the inequalities we have \begin{eqnarray*} 10&\geq&-0.5\cdot 8 + 5=1\\ 10&\geq&-1.25\cdot 8 + 8=-2, \end{eqnarray*} which is true.
The point $(10,-1)$ lies in region D: Substituting this point into the inequalities we have \begin{eqnarray*} -1&\leq&-0.5\cdot 10 + 5=0\\ -1&\geq&-1.25\cdot 10 + 8=-4.5, \end{eqnarray*} which is true.
-
We first observe that every point in the 3rd quadrant has negative $x$- and $y$-coordinates. So we have to show that for any point with negative $x$ and negative $y$ coordinates the two inequalities \begin{eqnarray*} y&\leq&-0.5 x + 5\\ y&\leq&-1.25 x + 8 \end{eqnarray*} are satisfied.
Note that for any negative value of $y$, the left hand side of both inequalities will be negative. Similarly, for any negative value of $x$, the right hand side of both inequalities will be positive. It is true that any negative number is smaller than any positive number. Therefore, both inequalities are satisfied for negative values of $x$ and $y$.
Solution Sets
Given below are the graphs of two lines, $y=-0.5 x + 5\ $ and $y=-1.25 x + 8,$ and several regions and points are shown. Note that $C$ is the region that appears completely white in the graph.

- For each region and each point, write a system of equations or inequalities, using the given two lines, that has the region or point as its solution set and explain the choice of $\leq,\, \geq$, or $=$ in each case. (You may assume that the line is part of each region.)
- The coordinates of a point within a region have to satisfy the corresponding system of inequalities. Verify this by picking a specific point in each region and showing that the coordinates of this point satisfy the corresponding system of inequalities for that region.
- In the previous part, we checked that specific coordinate points satisfied our inequalities for each region. Without picking any specific numbers, use the same idea to explain how you know that all points in the 3rd quadrant must satisfy the inequalities for region A.
