A Midpoint Miracle
Task
Draw a quadrilateral $ABCD$. Try to draw your quadrilateral so that no two sides are congruent, no two angles are congruent, and no two sides are parallel.
- Let $P$, $Q$, $R$, and $S$ be the midpoints of sides $AB$, $BC$, $CD$, and $DA$, respectively. Use a ruler to locate these points as precisely as you can, and join them to form a new quadrilateral $PQRS$. What do you notice about the quadrilateral $PQRS$?
- Suppose your quadrilateral $ABCD$ lies in the coordinate plane. Let $(x_1, y_1)$ be the coordinates of vertex $A$, $(x_2, y_2)$ the coordinates of $B$, $(x_3, y_3)$ the coordinates of $C$, and $(x_4, y_4)$ the coordinates of $D$. Use coordinates to prove the observation you made in part (a).
IM Commentary
This classroom task gives students the opportunity to prove a surprising fact about quadrilaterals: that if we join the midpoints of an arbitrary quadrilateral to form a new quadrilateral, then the new quadrilateral is a parallelogram, even if the original quadrilateral was not.
Student observations about the quadrilateral $PQRS$ in part (a) will vary. Some students may conjecture that the quadrilateral is a rhombus or rectangle, depending on how they drew the original quadrilateral. Teachers may find it helpful to have several students post the pictures they drew in part (a) in order to convince the class that while $PQRS$ always seems to be a parallelogram, it may not be a rhombus or rectangle.
One possible variant on part (a) is to have students draw the quadrilateral in GeoGebra, assuming that they have computers available. This allows students to move various parts of the quadrilateral around and see that the midpoint quadrilateral remains a parallelogram no matter where the parts are moved. This strategy also allows students to see that in general, the midpoint quadrilateral is not a rhombus or rectangle.
This fact provides an elegant example of a theorem in geometry that is somewhat tricky to prove using classical methods, but relatively easy to prove using coordinates. Students working on this task will have to use the formula for the midpoint of a line segment and the criterion for whether two lines are parallel (G-GPE.5).
Solutions
Solution: Solution
-
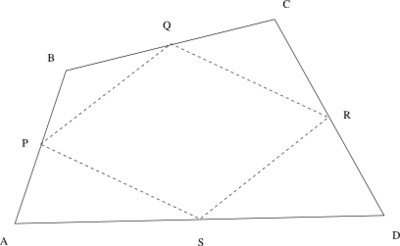
The quadrilateral PQRS appears to be a parallelogram. (In fact, in the picture above, it appears to be a rhombus, but if we draw a quadrilateral ABCD with two consecutive sides much shorter than the other two sides, we can see that the sides of PQRS need not be equal.) -
To prove that PQRS is a parallelogram, we will check that side PQ is parallel to SR and that QR is parallel to PS.
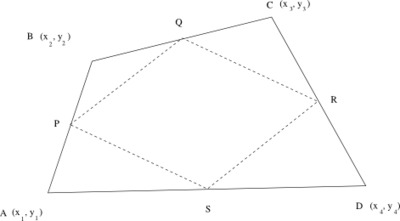
With the coordinates of A, B, C, and D as given above, we have \begin{eqnarray*} P & = & \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \\ Q & = & \left( \frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2} \right) \\ R & = & \left( \frac{x_3 + x_4}{2}, \frac{y_3 + y_4}{2} \right) \\ S & = & \left( \frac{x_4 + x_1}{2}, \frac{y_4 + y_1}{2} \right) \\ \end{eqnarray*} So the slope of the line PQ is \begin{eqnarray*} \frac{\Delta y}{\Delta x} & = & \frac{\frac{y_2 + y_3}{2} - \frac{y_1 + y_2}{2}}{\frac{x_2 + x_3}{2} - \frac{x_1 + x_2}{2}} \\ & = & \frac{(y_2 + y_3) - (y_1 + y_2)}{(x_2 + x_3) - (x_1 + x_2)} \\ & = & \frac{y_3 - y_1}{x_3 - x_1} \end{eqnarray*} The slope of the line SR is \begin{eqnarray*} \frac{\Delta y}{\Delta x} & = & \frac{\frac{y_3 + y_4}{2} - \frac{y_4 + y_1}{2}}{\frac{x_3 + x_4}{2} - \frac{x_4 + x_1}{2}} \\ & = & \frac{(y_3 + y_4) - (y_4 + y_1)}{(x_3 + x_4) - (x_4 + x_1)} \\ & = & \frac{y_3 - y_1}{x_3 - x_1} \end{eqnarray*} These slopes are the same; therefore, the lines PQ and SR are parallel. We can compute the slopes of lines QR and PS to find that both slopes are equal to $$ \frac{y_4 - y_2}{x_4 - x_2}. $$ Therefore, QR and PS are parallel as well. Since the quadrilateral PQRS has two pairs of parallel sides, it is a parallelogram.
Solution: Alternative Solution to (b)
We may simplify the algebraic work of this proof slightly by applying a transformation to the quadrilateral ABCD before we begin. Suppose that, by applying a translation and a rotation as necessary, we move the quadrilateral ABCD so that the vertex A is at the origin $(0, 0)$, and the vertex B is somewhere on the x-axis, at the point $(x_2, 0)$. We define $(x_3, y_3)$ and $(x_4, y_4)$ to be the new coordinates of the vertices C and D, respectively.
We now have \begin{eqnarray*} P & = & \left( \frac{x_2}{2}, 0 \right) \\ Q & = & \left( \frac{x_2 + x_3}{2}, \frac{y_3}{2} \right) \\ R & = & \left( \frac{x_3 + x_4}{2}, \frac{y_3 + y_4}{2} \right) \\ S & = & \left( \frac{x_4}{2}, \frac{y_4}{2} \right) \\ \end{eqnarray*} So the slope of the line PQ is \begin{eqnarray*} \frac{\Delta y}{\Delta x} & = & \frac{\frac{y_3}{2} - 0}{\frac{x_2 + x_3}{2} - \frac{x_2}{2}} \\ & = & \frac{y_3 - 0}{(x_2 + x_3) - x_2} \\ & = & \frac{y_3}{x_3} \end{eqnarray*} The slope of the line SR is \begin{eqnarray*} \frac{\Delta y}{\Delta x} & = & \frac{\frac{y_3 + y_4}{2} - \frac{y_4}{2}}{\frac{x_3 + x_4}{2} - \frac{x_4}{2}} \\ & = & \frac{(y_3 + y_4) - y_4}{(x_3 + x_4) - x_4} \\ & = & \frac{y_3}{x_3} \end{eqnarray*} These slopes are the same, so the lines PQ and SR are parallel. We can compute the slopes of lines QR and PS to find that both slopes are equal to $$ \frac{y_4}{x_4 - x_2}. $$ So QR and PS are parallel as well. Since the quadrilateral PQRS has two pairs of parallel sides, it is a parallelogram.
A Midpoint Miracle
Draw a quadrilateral $ABCD$. Try to draw your quadrilateral so that no two sides are congruent, no two angles are congruent, and no two sides are parallel.
- Let $P$, $Q$, $R$, and $S$ be the midpoints of sides $AB$, $BC$, $CD$, and $DA$, respectively. Use a ruler to locate these points as precisely as you can, and join them to form a new quadrilateral $PQRS$. What do you notice about the quadrilateral $PQRS$?
- Suppose your quadrilateral $ABCD$ lies in the coordinate plane. Let $(x_1, y_1)$ be the coordinates of vertex $A$, $(x_2, y_2)$ the coordinates of $B$, $(x_3, y_3)$ the coordinates of $C$, and $(x_4, y_4)$ the coordinates of $D$. Use coordinates to prove the observation you made in part (a).
