Task
Decompose teen numbers using 10-frames and a number equation.
Materials
- Number cards 11-19
- Pencil, crayon, or marker
- Attached student worksheet
Action
This activity can be done individually, in partners, or in small groups. The students have a teacher-made sheet and a writing implement. The cards are shuffled and placed face down.
 The student picks a card off of the top of the pile. The student then says the number and draws that many dots beginning with the first 10-frame. When the first 10-frame is filled, the student continues drawing the remaining dots in the next 10-frame. The student then fills in the blank equation with the corresponding numbers.
The student picks a card off of the top of the pile. The student then says the number and draws that many dots beginning with the first 10-frame. When the first 10-frame is filled, the student continues drawing the remaining dots in the next 10-frame. The student then fills in the blank equation with the corresponding numbers.
Example: 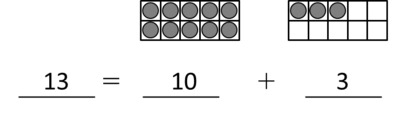
The student continues to pick cards and illustrate numbers in this way until all cards are used or the sheet is filled.
IM Commentary
The purpose of this task is to help students understand the base-ten structure of teen numbers. This task was designed specifically to support students in developing fluency with tens and teen numbers.
- Before starting this task, students should recognize that a full 10-frame represents 10 without having to count each dot, and also that a 10-frame can be partially filled to represent numbers less than 10.
- This activity can first be done orally, in a small teacher-led group or in pairs, using just the 10-frames and some counters.
- Students should know the meaning of the equals and plus signs if they are going to fill out the worksheet.
- Using a number line or number chart supports those students who do not know teen number names.
Computational fluency refers to having efficient, accurate, generalizable methods (algorithms) for computing numbers that are based on well-understood properties and number relationships (NCTM, 2000, p.144). Therefore, the focus in developing numeracy fluency should be more than the internalization of facts but on supporting students’ natural development of number sense so that they are able to solve computations flexibly and efficiently using their understanding of place value and relationships between numbers.
Children’s natural development of numbers progress from the concrete to the abstract, from counting all (e.g. physically making four counters and then making twelve and counting all the counters to get sixteen) to counting on (e.g. counting four more starting at twelve to get to sixteen( to using part-whole (e.g. splitting apart the twelve to ten and two, and adding the two to four, then adding the ten) and relational thinking (knowing that 4 + 10 is 14 so 4 + 9 would be just one less).
 The student picks a card off of the top of the pile. The student then says the number and draws that many dots beginning with the first 10-frame. When the first 10-frame is filled, the student continues drawing the remaining dots in the next 10-frame. The student then fills in the blank equation with the corresponding numbers.
The student picks a card off of the top of the pile. The student then says the number and draws that many dots beginning with the first 10-frame. When the first 10-frame is filled, the student continues drawing the remaining dots in the next 10-frame. The student then fills in the blank equation with the corresponding numbers.

