What is a Trapezoid? (Part 1)

Task

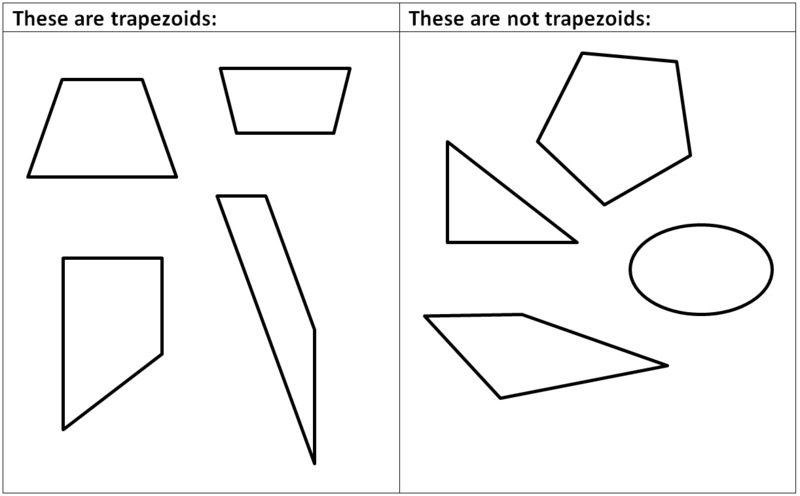
1. Say what a trapezoid is in your own words. Compare your definition with a partner.

2. Is this parallelogram a trapezoid according to your definition? Explain.

   

IM Commentary

The purpose of this task is for students to articulate a definition for a trapezoid. There are two competing definitions for "trapezoid":

• The exclusive definition of a trapezoid states that a trapezoid has exactly one pair of opposite sides parallel.

• The inclusive definition states that a trapezoid has at least one pair of opposite sides parallel.

Sometimes people say trapezoids "have one pair of opposite sides parallel," which leaves it ambiguous whether there can be more than one or not. The second part of the task pushes students to be clear about which version they intend. Because of the care students need to take with definitions, this task draws heavily on MP6, Attend to precision.

After students have articulated definitions for themselves or with a partner, the class should discuss the definition together. The class should decide on a single definition that they all agree on, as the point of having clearly articulated definitions is that we all know we are talking about the same thing. While both definitions are legitimate, the benefit to the inclusive definition is that any theorem proved true for a trapezoid is also true for a parallelogram. Furthermore, in their study The Classification of Quadrilaterals (Information Age Publishing, 2008), Usiskin et al. conclude,

The preponderance of advantages to the inclusive definition of trapezoid has caused all the articles we could find on the subject, and most college-bound geometry books, to favor the inclusive definition.

The inclusive definition sets up a relationship between parallelograms and trapezoids that is exactly analogous to to the relationship between squares and rectangles; the definition for rectangles includes squares in the same way that the inclusive definition of trapezoids includes parallelograms.

Please see the K-6 Geometry Progressions document for more information about these issues: http://commoncoretools.me/wp-content/uploads/2012/06/ccss_progression_g_k6_2012_06_27.pdf.

Solution

1. A trapezoid is a quadrilateral with one pair of opposite sides parallel. It can have right angles (a right trapezoid), and it can have congruent sides (isosceles), but those are not required.
2. Sometimes people define trapezoids to have at least one pair of opposite sides parallel, and sometimes say there is one and only one pair of opposite sides parallel. The parallelogram fits the "at least one" version of the definition because it has two pairs of opposite sides parallel, therefore it falls into the category of being both a trapezoid and a parallelogram. The parallelogram does not fit the "one and only one" version of the definition. So how students answer this depends on their definition.

Note: if students come up with different definitions, that is fine initially. However, in order to be able to discuss mathematical ideas going forward, the class should settle on one of these versions and go from there. See note in the commentary encouraging the version of the definition that includes parallelograms.