Kiri's Multiplication Matching Game
Task
The game is played with one to four players.
To play, two decks of cards are needed: the "matching" cards and the "target" cards.Â
An array of matching cards, which have numbers on their faces, is dealt face down. There can be twelve to twenty-four cards in the array. A single target card is dealt face up.
A turn consists of a student flipping over matching cards one at a time, then trying to combine them to meet the criterion of the target card. The quantity of flipped cards and method of combination can be varied to utilize different skills and give variety to the game. Two possible versions of the game are described below. The student wins a point if they state a correct mathematical relationship between the matching cards and the target card.
-
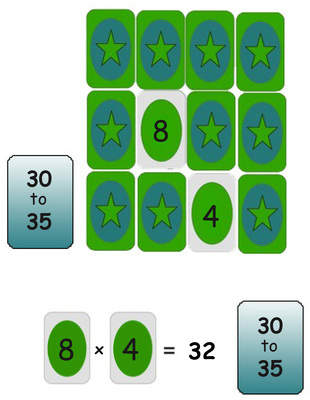
In one version, a player reveals two cards each turn. The player wins a point  if they can produce a product which matches the target card. Those who wish to keep track of points can do so by keeping target cards that are correctly "matched". Target cards can be single numbers but will more generally be descriptions of possible products. For example, the target card could be $24$, in which case the player would be looking for pairs $6$ and $4$, $8$ and $3$, or $12$ and $2$. But the target could also say "$30$ to $35$". In this case, if a player turns over a $4$, for example, they would then need to try to find an $8$, and to win the point they would need to say "$8$ times $4$ is $32$, which is between $30$ and $35$."
-
Another version of the game lets each player reveal three cards each turn. The player wins a point if they can produce an equation with their three cards and the target card that involves any of the operations of addition, subtraction, multiplication, or division. For example, suppose the target card is $7$ and the player turns $15$, $3$, and $2$. The player can win a point by stating that $15 \div 3 + 2 = 7$.
In each case, once a target card is "matched", a new target card is revealed. Â If a target card is not matched, the next player has a chance to match it. Â
Both of these versions of Kiri's Mathematical Match Game could be played as no-memory, light-memory, or memory games.
- In the no-memory version, the chosen matching cards are left face-up after they are revealed.
- In the light-memory version, the chosen matching cards are left face-up until some player is able to "match" the target card and wins a point.  When a match is made, all of the matching cards that are face-up are turned back face-down, the board is replenished, and a new target card is drawn, so the next player sees the initial set-up.
- In the memory version, the chosen matching cards are turned back face-down after every turn, so students would need to remember the locations of previously overturned cards in order to make use of them.
IM Commentary
This game is a fun way for the student to practice arithmetic skills to the point where the single-digit facts are committed to memory. It reinforces the relationship between multiplication and division, and depending on the target cards can also connect these recall skills with other skills such as estimation and understanding of properties. The only necessary materials, the cards, can be produced easily and can be re-used.  After playing regularly, students could be engaged in making new target cards.
Here are some guidelines for constructing the "matching" and "target" card decks. The matching cards should typically be labeled between $1$ and $10$ or $12$.  Larger numbers are possible, especially for variants that also involve addition. The target cards should be constructed to give a few possibilities, and promote reflection. For example, a target card might be just a single integer, but if so it should probably have many factors or else the game would proceed too slowly. A target card could be a small range of integers, such as "30 to 35". The targets can be even more interesting, too. For example, a target of "ones digit is $5$" invites students to notice that for this target, one of the two factors must be a $5$, and the other must be odd.  The target card deck can be varied to encourage using different skills.
The second version of the game described in this task requires the student to process, if they are flipping three cards, up to $96$ possible arithmetic expressions (not counting commutativity) for matching the target card. Going through many of those possibilities fluidly would indicate a strong level of proficiency not only in multiplication facts but in use of properties as well.
Points could be ignored entirely, or used to determine "winners", or could be used to earn rewards collectively or individually.
This is a third-grade version of 1.OA Kiri's Mathematical Match Game.
Solution
Students meet the basic mathematical requirements of the game by evaluating products within $100$. To play the game fluidly and successfully, students will need most products committed to memory. If students are not already at this level, the versions of the game described in this task can help them commit these facts to memory while also allowing them to compute more quickly by recognizing patterns and structure in arithmetic.
Kiri's Multiplication Matching Game
The game is played with one to four players.
To play, two decks of cards are needed: the "matching" cards and the "target" cards.Â
An array of matching cards, which have numbers on their faces, is dealt face down. There can be twelve to twenty-four cards in the array. A single target card is dealt face up.
A turn consists of a student flipping over matching cards one at a time, then trying to combine them to meet the criterion of the target card. The quantity of flipped cards and method of combination can be varied to utilize different skills and give variety to the game. Two possible versions of the game are described below. The student wins a point if they state a correct mathematical relationship between the matching cards and the target card.

-
In one version, a player reveals two cards each turn. The player wins a point  if they can produce a product which matches the target card. Those who wish to keep track of points can do so by keeping target cards that are correctly "matched". Target cards can be single numbers but will more generally be descriptions of possible products. For example, the target card could be $24$, in which case the player would be looking for pairs $6$ and $4$, $8$ and $3$, or $12$ and $2$. But the target could also say "$30$ to $35$". In this case, if a player turns over a $4$, for example, they would then need to try to find an $8$, and to win the point they would need to say "$8$ times $4$ is $32$, which is between $30$ and $35$."
-
Another version of the game lets each player reveal three cards each turn. The player wins a point if they can produce an equation with their three cards and the target card that involves any of the operations of addition, subtraction, multiplication, or division. For example, suppose the target card is $7$ and the player turns $15$, $3$, and $2$. The player can win a point by stating that $15 \div 3 + 2 = 7$.
In each case, once a target card is "matched", a new target card is revealed. Â If a target card is not matched, the next player has a chance to match it. Â
Both of these versions of Kiri's Mathematical Match Game could be played as no-memory, light-memory, or memory games.
- In the no-memory version, the chosen matching cards are left face-up after they are revealed.
- In the light-memory version, the chosen matching cards are left face-up until some player is able to "match" the target card and wins a point.  When a match is made, all of the matching cards that are face-up are turned back face-down, the board is replenished, and a new target card is drawn, so the next player sees the initial set-up.
- In the memory version, the chosen matching cards are turned back face-down after every turn, so students would need to remember the locations of previously overturned cards in order to make use of them.
