Adding Base Ten Numbers, Part 1
Task
The diagram below can be used to represent 40 + 80 = 120 Â if a small square represents 10 and a group of ten squares represents 100:

It can also represent 0.04 + 0.08 = 0.12Â if a small square represents 0.01Â and a group of ten squares represents 0.1.
- Name at least two more sums it can represent. What does a small square represent? What does a group of ten squares represent?Â
Draw a diagram to represent each of the following sums. Describe what the small squares in your diagram represent.
- 0.005 + 0.002
- 0.0008Â + 0.0006
- 0.00007 + 0.00003
IM Commentary
This is the first in a set of three tasks generalizing the addition algorithm shown below from whole numbers to all base-ten numbers. [Part 1, Part 2, Part 3]
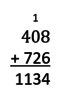
The goal of this task is to demonstrate that since digits in the same place represent the same-sized units, we can always add digits in the same place. If they sum to more than ten, the ten units can be bundled together into a unit that goes with the place to the left, which we represent by placing a 1 in the place to the left. The idea in the given diagram (addition and place value with regrouping) should be familiar to students. In grade 5, students worked with decmals to the hundredths place. This task builds on existing understanding to show that the idea generalizes to any place in a base-ten number.
In part (a), there is nothing stopping students from deciding that a square can represent any value (as shown in a.iv. in the solution below). While this approach should be acknowledged as correct, it doesn't support the goal of generalizing steps in the algorithm. Classroom discussion should focus on solutions where a square represents a power of ten.
Solution
- Answers will vary. Some possibilities are:
- The diagram could represent 4 + 8 = 12, if a small square represents 1 and a group of ten represents 10.
- The diagram could represent 400 + 800 = 1200, if a small square represents 100 and a group of ten represents 1000.
- The diagram could represent 0.4 + 0.8 = 1.2, if a small square reprsents 0.1 and a group of ten represents 1.
- The diagram could represent 20 + 40 = 60, if a small square represents 5 and a group of ten represents 50. (Note that this is correct, but not helpful for understanding how the algorithm generalizes.)
- In this diagram, the small squares represent 0.001. The sum is 0.007.Â

- In this diagram, the small squares represent 0.0001. The large rectangle encloses ten squares, and the group of ten squares represents 0.001. The sum is 0.0014.Â

- In this diagram, the small squares represent 0.00001. The large rectangle shows that it contains ten squares. The sum is 0.0001. It would also be acceptable to write 0.00010.Â

Adding Base Ten Numbers, Part 1
The diagram below can be used to represent 40 + 80 = 120 Â if a small square represents 10 and a group of ten squares represents 100:

It can also represent 0.04 + 0.08 = 0.12Â if a small square represents 0.01Â and a group of ten squares represents 0.1.
- Name at least two more sums it can represent. What does a small square represent? What does a group of ten squares represent?Â
Draw a diagram to represent each of the following sums. Describe what the small squares in your diagram represent.
- 0.005 + 0.002
- 0.0008Â + 0.0006
- 0.00007 + 0.00003
