Adding Base Ten Numbers, Part 2
Task
Add:
- 4,000 + 5,000
- 600 + 200
- 20 + 50
- 8 + 1
- 0.3 + 0.4
- 0.07 + 0.02
- 0.001 + 0.006
- 0.0005Â + 0.0003
- 4628.3715 + 5251.4263
Add some more:
- 600 + 700
- 0.005Â + 0.008
- 600.005Â + 700.008
IM Commentary
This is the second in a set of three tasks generalizing the addition algorithm shown below from whole numbers to all base-ten numbers. [Part 1, Part 2, Part 3]
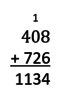
In the first set of sums, no regrouping is required. Items (a) through (f) involve addition problems students may have seen in previous grades; then students engage in a mild version of MP8 as this repeated reasoning is extended to decimals beyond the hundredths place. Students may simply use their understanding of the place value system to write sums, or some students may need to draw diagrams akin to Part 1 to support their reasoning. In part (i), students handle digits appearing in multiple places in the addends, though still with no regrouping. If students don't notice organically, a teacher can promote fluency in reading numbers by pointing out that part (i) consists of adding up the sums from parts (a) through (h).
Parts (j) through (l) put everything together with a numerical example. First students make sense of regrouping beyond the hundredths place, and then deal with regrouping given addends with digits in different places.
A nice extension of this task would be to ask the question in the opposite direction: give students a number and ask them to come up with two numbers that add up to it. (For example: "Come up with two numbers that sum to 12.015.") Groups could write their responses on a board or share them on something like Padlet, so that everyone can see all the different ways of thinking.Â
Solution
Add:
- 4,000 + 5,000 = 9,000
- 600 + 200 = 800
- 20 + 50 = 70
- 8 + 1 = 9
- 0.3 + 0.4 = 0.7
- 0.07 + 0.02 = 0.09
- 0.001 + 0.006 = 0.007
- 0.0005Â + 0.0003Â = 0.0008
- 4628.3715 + 5251.4264 = 9879.7978
Add some more:
- 600 + 700 = 1,300
- 0.005Â + 0.008 = 0.013
- 600.005Â + 700.008 = 1,300.013
Adding Base Ten Numbers, Part 2
Add:
- 4,000 + 5,000
- 600 + 200
- 20 + 50
- 8 + 1
- 0.3 + 0.4
- 0.07 + 0.02
- 0.001 + 0.006
- 0.0005Â + 0.0003
- 4628.3715 + 5251.4263
Add some more:
- 600 + 700
- 0.005Â + 0.008
- 600.005Â + 700.008
