When Does SSA Work to Determine Triangle Congruence?

Task

Josh is told that two triangles $ABC$ and $DEF$ share two sets of congruent sides and one pair of congruent angles: $AB$ is congruent to $DE$, $BC$ congruent to $EF$, and angle $C$ is congruent to angle $F$. He is asked if these two triangles must be congruent. Josh draws the two triangles below and says "They are definitely congruent because they share all three side lengths!''

1. Explain Josh's reasoning using one of the triangle congruence criteria: ASA, SSS, SAS.
2. Give an example of two triangles $ABC$ and $DEF$, fitting the criteria of this problem, which are not congruent.

IM Commentary

The triangle congruence criteria, SSS, SAS, ASA, all require three pieces of information. It is interesting, however, that not all three pieces of information about sides and angles are sufficient to determine a triangle up to congruence. In this problem, we considered SSA. Also insufficient is AAA, which determines a triangle up to similarity. Unlike SSA, AAS is sufficient because two pairs of congruent angles force the third pair of angles to also be congruent.

We also saw in Josh's example that if the corresponding angles $C$ and $F$ are right angles then the two triangles $ABC$ and $DEF$ are necessarily congruent. Interestingly, the same conclusion holds if the angles are obtuse: in order for the example given in the answer to part (b) to work, it is necessary that the perpendicular from $A$ to line $BC$ meets $BC$ between $B$ and $C$ and this will fail if angle $B$ is obtuse:

Solutions

Solution: 1 Pythagorean Theorem

1. Josh's reasoning is incorrect because he has made the unwarranted assumption that angles C and F are right angles. However, with that additional assumption his statement is correct, since we may apply the Pythagorean theorem to conclude that

   $$ |AC|^2 = |AB|^2 - |BC|^2 \quad \text{and} \quad |DF|^2 = |DE|^2 - |EF|^2. $$

   Since $DE$ is congruent to $AB$ and $EF$ is congruent to $BC$ by hypothesis we can conclude that $AC$ must be congruent to $DF$ and so, by SSS, triangle $ABC$ is congruent to triangle $DEF$. Instead of SSS, we could also apply SAS using right angles $C$ and $F$ along with sides $AC$ and $BC$ for triangle $ABC$ and sides $DF$ and $EF$ for triangle $DEF$.

2. The information given amounts to SSA, two congruent sides and a congruent angle which is notthe angle determined by the two sets of congruent sides. This is a lot of information and, as might be expected, does not leave much ambiguity. Consider five points $A$, $B$, $C$, $D$, $E$ as pictured below with isosceles triangle $ADE$:

   

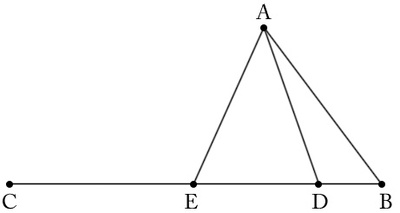
   Triangles $ABD$ and $ABE$ share angle $B$ and side $AB$ while $AD$ is congruent to $AE$ by construction. The triangles $ABD$ and $ABE$ are definitely not congruent, however, as one of them is properly contained within the other.

   The given information heavily restricted this construction but we were still still able to find two non congruent triangles sharing two congruent sides and a non-included congruent angle.

Solution: Approach via Rigid Motions

1. Suppose first that we assume, as drawn in the picture, that $A,C,F,$ and $D$ are collinear. Then let $R$ be the midpoint of $\overline{CF}$ and let $l$ be the line perpendicular to line $AD$ at $R$ as pictured below:

   
   
   

   

   We reflect triangle $ABC$ about $l$ and call its image $GHI$. The goal is to show that the two triangles $GHI$ and $DEF$ are the same. Since $R$ is the midpoint of $\overline{CF}$ and $l$ is perpendicular to line $CF$ we know that reflection about $l$ maps $C$ to $F$. This tells us that $I = F$. Reflection about $l$ also preserves angles so that angle $GIH$ is a right angle. We already know that $I = F$ and there is only one right angle with leg $\overline{DF}$ whose other leg lies above line $DF$ so ray $IH$ is the same as ray $FE$. By hypothesis, $FE$ and $CB$ are congruent and reflection preserves segment lengths so we conclude that $FE$ is the same segment as $IH$.

   We finally need to show that $G=D$ so that our two triangles $DEF$ and $GHI$ are the same. We know that $G$ is on line $DF$ and $|DE| = |GE|$. The circle with radius $|DE|$ and center $E$ meets line $DE$ in $D$ and in one other point which is the reflection of $D$ across line $EF$. Since $G$ is on the same side of line $EF$ as $D$ by construction it must be that $G = D$.

   We now return to deal with the possibility that $A,C,D,$ and $F$ are not collinear. Suppose point $C$ is not on line $DF$. Let $P$ be the point on line $DF$ so that lines $PC$ and $DF$ are perpendicular. Translating triangle $ABC$ by segment $CP$ we find triangle $NOP$ where $P,D$ and $F$ are collinear and $N,O$ are the images of $A,B$ by translation by $PC$. If $N$ is also on line $DF$ then the argument in the collinear case can be applied directly. If not, then rotating triangle $NOP$ about $P$ by angle $NOQ$, where $Q$ is on line $DF$ and $F$ is between $Q$ and $D$ gives a new triangle for which we can apply the argument above.