Do two points always determine a linear function?
Task
- Suppose $P_1 = (0,5)$ and $P_2 = (3,−3)$. Sketch $P_1$ and $P_2$. For which real numbers $m$ and $b$ does the graph of a linear function described by the equation $f(x) = mx+b$ contain $P_1$? Explain. Do any of these graphs also contain $P_2$? Explain.
- Suppose $P_1 = (0,5)$ and $P_2 = (0,7)$. Sketch $P_1$ and $P_2$. Are there real numbers $m$ and $b$ for which the graph of a linear function described by the equation $f(x)=mx+b$ contains $P_1$ and $P_2$? Explain.
- Now suppose $P_1= (c,d)$ and $P_2 = (g,h)$ and $c$ is not equal to $g$. Show that there is only one real number $m$ and only one real number $b$ for which the graph of $f(x)=mx+b$ contains the points $P_1$ and $P_2$.
IM Commentary
In a geometric context, two distinct points $P_1$and $P_2$ always determine a unique line in the Cartesian plane (this is one of the basic postulates of Euclidean geometry). Only the non-vertical lines, however, can be described by the graph of a function $f(x) = mx + b$. This task focuses on producing an explicit function $f(x)$ in the case where the line is not vertical.
This problem allows the student to think geometrically about lines and then relate this geometry to linear functions. Or the student can work algebraically with equations in order to find the explicit equation of the line through two points (when that line is not vertical).
Solutions
Solution: 1
-
The graph of the linear function described by $f(x) = mx + b$ contains $(0,5)$ when the $y$-intercept of the graph, given by $b$, is equal to $5$. So the linear functions whose graph contains $(0,5)$ are those of the form $$ f(x) = mx + 5 $$ where $m$ is a real number.
In order for the graph of $f$ to contain $(3,-3)$ we need $$ -3 = f(3) = 3m + 5. $$ Solving for $m$ gives $$ m = -\frac{8}{3}. $$ So there is only one linear function whose graph passes through $(0,5)$ which also passes through $(3,-3)$, namely the one described by $$ f(x) = -\frac{8}{3}x + 5, $$ depicted below.
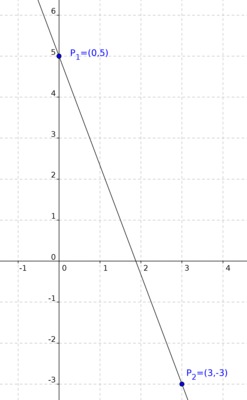
-
If $f$ is any function, then its graph consists of the pairs $(x,f(x))$. So
for each $x$-value there can only be one associated $f(x)$-value which is
on the graph of $f$. In this case $(0,5)$ and $(0,7)$ both have $x$-value zero
and so these two points cannot be on the graph of any function, whether or not
the function is linear.

-
Asking for the point $P_1 = (c,d) $ to be on the graph of $f(x) = mx + b$ means that $$ d = mc + b. $$ Similarly asking for the point $P_2 = (g,h) $ to be on the graph of $f(x) = mx + b$ means that $$ h = mg + b. $$ Subtracting the second equation from the first gives $$ d - h = m(c - g) $$ so $$ m = \left(\frac{d-h}{c - g}\right). $$ Note that the expression for the slope $m$ only makes sense if $c \neq g$, which has been assumed in the problem. Once we have found $m$ we can plug this into one of the equations(either for $d$ or for $h$) and then solve for $b$: $$ d = \left(\frac{d - f}{c - g}\right) c + b. $$ Solving for $b$ gives $$ b = d-\left(\frac{d-h}{c-g}\right)c. $$ So with the hypothesis that $c \neq g$ there is a linear function whose graph contains $P_1$ and $P_2$ namely $$ f(x) = \left(\frac{d-h}{c-g}\right)x + d -\left(\frac{d-f}{c-g}\right)c. $$
Finally, we note that we have also that there is a unique such line, as any line containing $P_1$ and $P_2$ must have the slope and $y$-intercept as calculated above. Explicitly: If there were a different linear function $g(x) = m_1x + b_1$ whose graph contained $P_1$ and $P_2$, then by virtue of it containing $P_1$ we must have $$ d = m_1c + b_1. $$ Similarly, since the graph of $g$ contains $P_2$, we must have $$ h = m_1g + b_1. $$ These two allow us to solve for $m_1$, as above, and we find the same solution, namely $$ m_1 = \left(\frac{d-h}{c - g}\right). $$ We then find, also as above, that $b_1 = b$ and so $g(x) = f(x)$: there is only one linear equation of the form $f(x) = mx + b$ whose graph contains $P_1$ and $P_2$.
Solution: 2 Thinking Geometrically
From a geometric point of view, we can see the answer to part (c) as follows. Given the two points $P_1$ and $P_2$ we can draw the unique line containing these two points. If $f_1(x) = m_1x + b_1$ and $f_2(x) = m_2x + b_2$ were two equations whose graphs describe this line, this means that $$ m_1x + b_1 = m_2x + b_2 $$ for all values of $x$. This is only possible if $m_1 = m_2$ and $b_1 = b_2$ as we can see, for example, by rewriting this equation as $$ (m_1-m_2)x = b_2 - b_1. $$ The right hand side of this equation does not depend on $x$ so this forces $m_1 - m_2 = 0$ and once $m_1 = m_2$ then the left hand side is zero, forcing $b_1 = b_2$.
Do two points always determine a linear function?
- Suppose $P_1 = (0,5)$ and $P_2 = (3,−3)$. Sketch $P_1$ and $P_2$. For which real numbers $m$ and $b$ does the graph of a linear function described by the equation $f(x) = mx+b$ contain $P_1$? Explain. Do any of these graphs also contain $P_2$? Explain.
- Suppose $P_1 = (0,5)$ and $P_2 = (0,7)$. Sketch $P_1$ and $P_2$. Are there real numbers $m$ and $b$ for which the graph of a linear function described by the equation $f(x)=mx+b$ contains $P_1$ and $P_2$? Explain.
- Now suppose $P_1= (c,d)$ and $P_2 = (g,h)$ and $c$ is not equal to $g$. Show that there is only one real number $m$ and only one real number $b$ for which the graph of $f(x)=mx+b$ contains the points $P_1$ and $P_2$.
