How Many Containers in One Cup / Cups in One Container?
Task
-
If $\frac12$ cup of water fills $\frac23$ of a plastic container, how many containers will 1 cup fill?
-
Solve the problem by drawing a picture.
-
Which of the following multiplication or divisions problems represents this situation? Explain your reasoning.
$$\frac12 \times \frac23=? \qquad \frac12 \div \frac23=? \qquad \frac23 \div \frac12=? $$ Solve the arithmetic problem you chose in part (3) and verify that you get the same answer as you did with your picture.
-
-
If $\frac12$ cup of water fills $\frac23$ of a plastic container, how many cups of water will the full container hold?
-
Solve the problem by drawing a picture.
-
Which of the following multiplication or divisions equations represents this situation? Explain your reasoning.
$$ \frac12 \times \frac23=? \qquad \frac12 \div \frac23=? \qquad \frac23 \div \frac12=? $$ Solve the arithmetic problem you chose in part (3) and verify that you get the same answer as you did with your picture.
-
IM Commentary
These two fraction division tasks use the same context and ask “How much in one group?†but require students to divide the fractions in the opposite order. Students struggle to understand which order one should divide in a fraction division context, and these two tasks give them an opportunity to think carefully about the meaning of fraction division.
The purpose of this problem is to help students deepen their understanding of the meaning of fractions and fraction division and to see that they get the same answer using standard algorithm as they do just reasoning through the problem. Later they can build on this to explain why dividing by, for example, $\frac23$ is the same as multiplying by $\frac32$ based on the meaning of multiplication and division by fractions.
Solution
-
-
Below is a series of pictures that can be used to solve the problem as well as an explanation of what the picture represents at each step.
$\frac12$cup of water fills $\frac23$ of a plastic container, as shown below.

We know that $\frac12$ cup of water fills $\frac23$ of a plastic container. The question is asking, "How many containers can be filled with 1 cup of water." Since 1 cup of water is twice as much as $\frac12$ cup of water, we know that 1 cup of water will fill twice as much of a container.
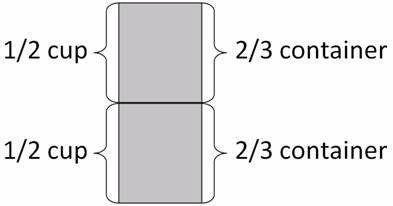
The answer to the question can easily be found by relabeling the above picture.
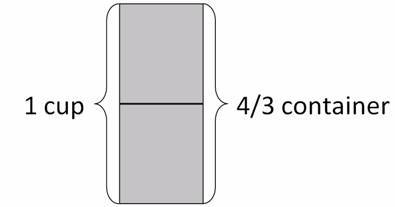 Twice as much water will fill twice as many containers. Thus, 1 cup of water will fill $\frac43$ of a container.
Twice as much water will fill twice as many containers. Thus, 1 cup of water will fill $\frac43$ of a container.
Â
-
We are looking for the number of containers filled by 1 cup, and we know $\frac12$ of that unknown amount fills $\frac23$ of a container. We can write this symbolically as $$\frac12 \times ? = \frac23$$ which is equivalent to $\frac23 \div \frac12$ Computing this by multiplying by the reciprocal, we find that $$ \begin{align} \frac23 \div \frac12 &=\\ &=\frac23 \times \frac21 \\ &= \frac43 \end{align} $$
-
When we solved the problem with a picture, we took the fraction of the container filled by $\frac12$ cup and doubled it to find the fraction of a container filled by one cup. This is exactly what we did when we did it through computations: to divide $\frac23$ by $\frac12$ we multiplied it by 2. The two ways of solving it do result in the same answer and even follow the same process.
-
-
-
Below is a series of pictures that can be used to solve the problem as well as an explanation of what the picture represents at each step.
$\frac12$ cup fills $\frac23$ of the container, as shown in the picture below.

Since the picture represents $\frac23$ of the container, $\frac12$ of $\frac23$ will be $\frac13$ of the container. In the picture below, each piece represents $\frac12$ of $\frac23$, and also represents $\frac12$ of $\frac12$. Since $\frac12 \times \frac12 = \frac14$, each piece also represents $\frac14$ cup.

We have $\frac23$ of the container, but we need to know how many cups it takes to fill $\frac33$ of the container, so if we take 3 of the thirds, we will have the amount of water needed for the full container. This is the same thing as multiplying $3 \times \frac14$.

We can see that $\frac34$ cup is needed to fill the whole container.
-
We are looking for the number of cups needed to fill one container, and we know $\frac23$ of that unknown amount requires $\frac12$ a cup. We can write this symbolically as $$\frac23 \times ? = \frac12$$ which is equivalent to $\frac12 \div \frac23$ Computing this by multiplying by the reciprocal, we find that $$ \begin{align} \frac12 \div \frac23 &=\\ &=\frac12 \times \frac32 \\ &= \frac34 \end{align} $$
-
When we solved the problem using a picture, we found $\frac12$ of the amount (because we knew it was 2 thirds of the container, and so $\frac12$ of that would be 1 third of the container) and then we multiplied that amount by 3 to get the amount in the whole container. This is exactly what we did when we multiplied by the reciprocal of $\frac23$: multiplying by $\frac12$ and then by $3$ is the same as multiplying by $\frac32$. So whether we solve it with a picture or via computation, we get the same answer (in fact, the process itself is the same).
-
How Many Containers in One Cup / Cups in One Container?
-
If $\frac12$ cup of water fills $\frac23$ of a plastic container, how many containers will 1 cup fill?
-
Solve the problem by drawing a picture.
-
Which of the following multiplication or divisions problems represents this situation? Explain your reasoning.
$$\frac12 \times \frac23=? \qquad \frac12 \div \frac23=? \qquad \frac23 \div \frac12=? $$ Solve the arithmetic problem you chose in part (3) and verify that you get the same answer as you did with your picture.
-
-
If $\frac12$ cup of water fills $\frac23$ of a plastic container, how many cups of water will the full container hold?
-
Solve the problem by drawing a picture.
-
Which of the following multiplication or divisions equations represents this situation? Explain your reasoning.
$$ \frac12 \times \frac23=? \qquad \frac12 \div \frac23=? \qquad \frac23 \div \frac12=? $$ Solve the arithmetic problem you chose in part (3) and verify that you get the same answer as you did with your picture.
-
