Triangle Series
Task
Consider the picture below, consisting of a nested sequence of five equilateral triangles, colored in black. Each of the black triangles is made by connecting the three midpoints of the sides of the immediately larger white triangle.
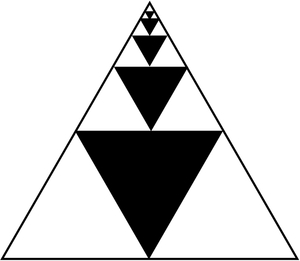
Find and evaluate a sum to compute the total area of the black region (that is, the sum of the areas of the five black triangles) given that the largest triangle in the diagram has area 1.
IM Commentary
The purpose of this task is to emphasize the adjective "geometric" in the "geometric" series, namely, that the algebraic notion of a common ratio between terms corresponds to the geometric notion of a repeated similarity transformation. Specifically, since the black triangles are all similar with the same scale factor, the total area of the black triangles is a geometric series. This task could be used either to introduce the geometric series as a worthy object of study, or as a geometric application of its use.
Solution
The geometric key to the task is to note that of the various equilateral triangle sizes in the problem, each has $\tfrac{1}{4}$ the area of the immediately larger triangle of which it is a part (since each smaller such triangle has half its base and half its height).
In particular, the area of the largest black triangle (and each of the white triangles of the same size) is $\tfrac{1}{4}$ of the area of the large triangle, i.e., $\frac{1}{4}(1)=\frac{1}{4}$. Similarly, the second largest black triangle has $\frac{1}{4}$ the area of one of these white triangles, so has area $\tfrac{1}{4}\cdot\tfrac{1}{4}=\frac{1}{4^2}.$ Continuing in this way, the third, fourth, and fifth black triangles have respective areas $\frac{1}{4^3}$, $\frac{1}{4^4}$, and $\frac{1}{4^5}$. The sum of the areas of the black triangles can now be evaluated by the formula for a finite geometric series (with common ratio $\tfrac{1}{4}$): \begin{align} \text{Black Area} &= \frac{1}{4}+\frac{1}{4^2}+\frac{1}{4^3}+\frac{1}{4^4}+\frac{1}{4^5}\\ &=\frac{1}{4}\left(1+\frac{1}{4}+\frac{1}{4^2}+\frac{1}{4^3}+\frac{1}{4^4}\right)\\ &=\frac{1}{4}\cdot\frac{1-\frac{1}{4}^5}{1-\frac{1}{4}}\\ &=\frac{341}{1024}. \end{align}
Triangle Series
Consider the picture below, consisting of a nested sequence of five equilateral triangles, colored in black. Each of the black triangles is made by connecting the three midpoints of the sides of the immediately larger white triangle.

Find and evaluate a sum to compute the total area of the black region (that is, the sum of the areas of the five black triangles) given that the largest triangle in the diagram has area 1.
