Jim and Jesse's Money
Task
Jim and Jesse each had the same amount of money. Jim spent $\$58$ to fill the car up with gas for a road-trip. Jesse spent $\$37$ buying snacks for the trip. Afterward, the ratio of Jim’s money to Jesse’s money is $1:4$. How much money did each have at first?
Solutions
Solution: Use two bar diagrams
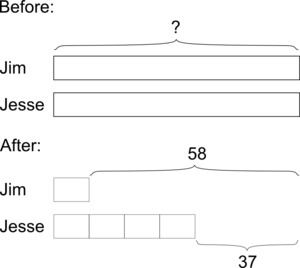
We know that Jesse has \$21 more than Jim after they make their purchases, because Jim spent \$21 more than Jesse. Since the ratio of money they have remaining is $1:4$, we know this difference is 3 times what Jim has left.
$3 \text{ units } = \$58 - \$37 = \$21$
$1 \text{ unit } = \$7$
We should add what Jim has left to what he spent:
$\$58 + \$7 = \$65$
They each had $\$65$ at first.
Solution: Same story, slightly different analysis
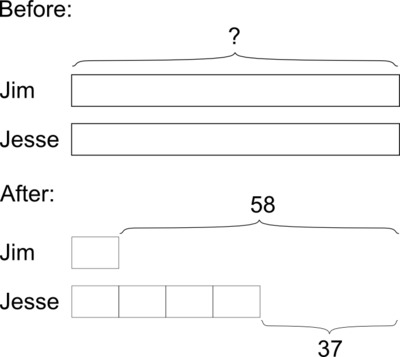
We know that Jim spent \$21 more than Jesse, so Jim has \$21 less than Jesse after they make their purchases. Since Jim has only $\frac14$ as much money as Jesse has, the difference between the two amounts is $\frac34$ of the amount of money Jesse has. So 21 is $\frac34$ of the amount of money Jesse has. Therefore, $\frac14$of the amount of money Jesse has is one third of this, or 7. So Jesse has $4 \cdot 7=28$; and since he spent 37, he originally had $28 + 37=65$. So Jim and Jesse each originally had \$65.
Jim and Jesse's Money
Jim and Jesse each had the same amount of money. Jim spent $\$58$ to fill the car up with gas for a road-trip. Jesse spent $\$37$ buying snacks for the trip. Afterward, the ratio of Jim’s money to Jesse’s money is $1:4$. How much money did each have at first?
