The Parking Lot

Task

A parking lot charges $\$0.50$ for each half hour or fraction thereof, up to a daily maximum of $\$10.00$. Let $C(t)$ be the cost in dollars of parking for $t$ minutes.

1. Complete the table below.

   $t$ (minutes)	$C(t)$ (dollars)
   0
   $15$
   $20$
   $35$
   $75$
   $125$

2. Sketch a graph of $C$ for $0 \leq t \leq 480$.
3. Is $C$ a function of $t$? Explain your reasoning.
4. Is $t$ a function of $C$? Explain your reasoning.

IM Commentary

The purpose of this task is to investigate the meaning of the definition of function in a real-world context where the question of whether there is more than one output for a given input arises naturally. In more advanced courses this task could be used to investigate the question of whether a function has an inverse.

Solution

1. $t$ (minutes)	$C(t)$ (dollars)
   0	0
   $15$	$0.50$
   $20$	$0.50$
   $35$	$1.00$
   $75$	$1.50$
   $125$	$2.50$

   As a sample calculation, we note that $125$ minutes is two full hours (four half-hours) and part of another half hour. Since the ticketing scheme rounds up to the nearest half-hour, we have to pay for five half-hours, at a total cost of $2.50.
2. 
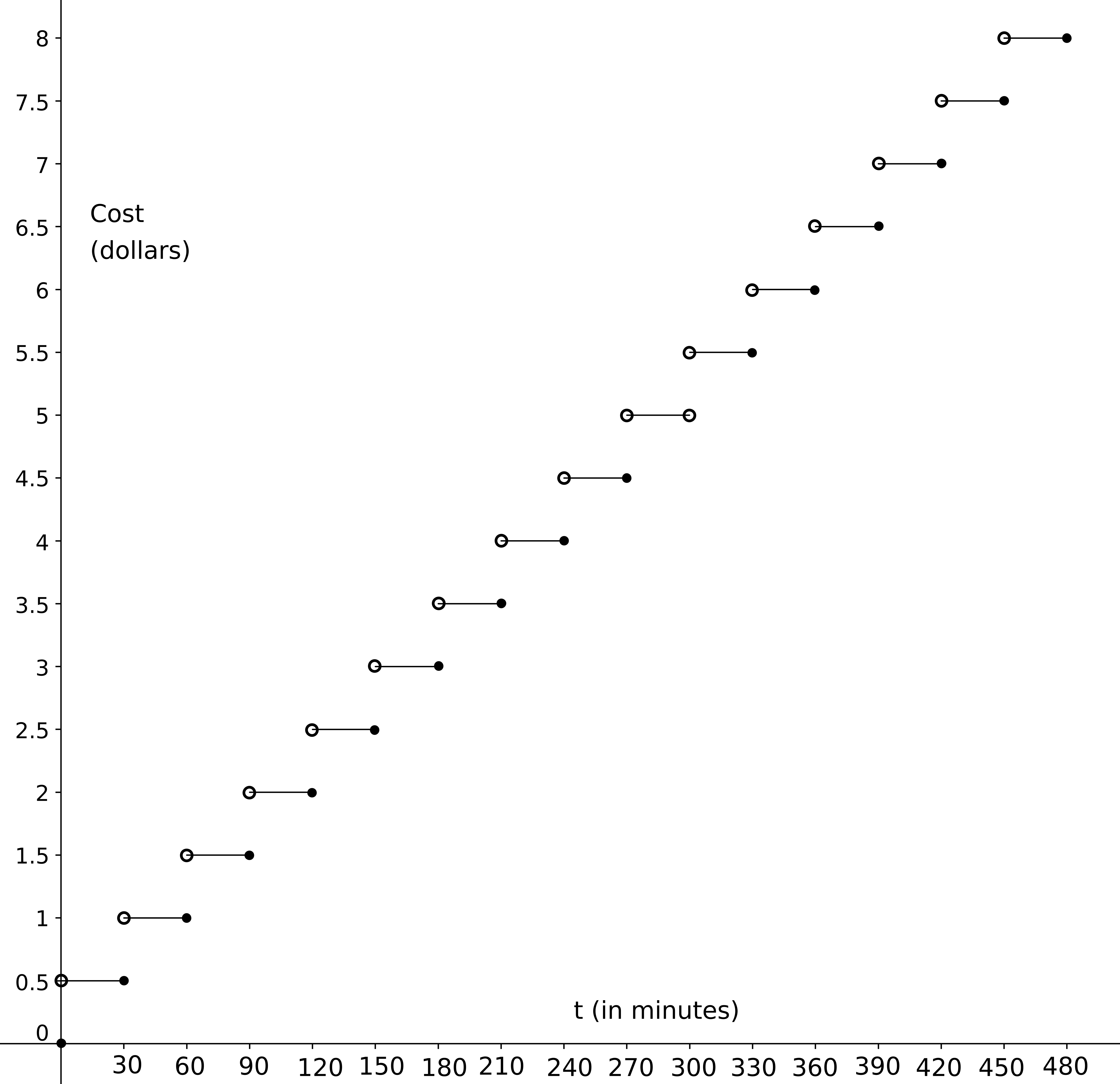
3. Yes, $C$ is a function of $t$ because for a given parking time of $t$ minutes there is exactly one charge.
4. No, $t$ is not a function of $C$ because there are values of $C$ that have many values of $t$ associated with them. For example if you end up paying $\$0.50$ then you could have parked for any period of time up to half an hour, that is, when $C = 0.50$ then $t$ can have any value in the range $0 < t \le 30$. So the "input" $C = 0.50$ yields more than one output, which is not allowed for a function.