Graphs of Power Functions
Task
Sketch the graphs of the functions described by $\displaystyle f(x)=x^2$ and $\displaystyle g(x)=x^4$ on the same axes, being careful to label any points of intersection. Also, find and label $\displaystyle\left(\frac{1}{2}, f(\frac{1}{2})\right)$ and $\displaystyle\left(\frac{1}{2}, g(\frac{1}{2})\right)$.
Sketch the graphs of the functions described by $f(x)=x^3$ and $g(x)=x^5$ on the same axes, being careful to label any points of intersection. Also, find and label $\displaystyle\left(\frac{1}{2}, f(\frac{1}{2})\right)$ and $\displaystyle\left(\frac{1}{2}, g(\frac{1}{2})\right)$.
Sketch the graphs of the functions described by $f(x)=x^2$ and $g(x)=x^3$ on the same axes, being careful to label any points of intersection. Also, find and label $\displaystyle\left(\frac{1}{2}, f(\frac{1}{2})\right)$ and $\displaystyle\left(\frac{1}{2}, g(\frac{1}{2})\right)$.
IM Commentary
This task requires students to recognize the graphs of different (positive) powers of $x$. There are several important aspects to these graphs. First, the graphs of even powers of $x$ all open upward as $x$ grows in the positive or negative direction. The larger the even power, the flatter these graphs look near $0$ and the more rapidly they increase once the distance of $x$ from $0$ excedes $1$. For an odd power of $x$ the value of the function is positive when $x$ is positive and negative when $x$ is negative. As in the even case, the larger the odd exponent, the flatter the graph is near $x = 0$ and the steeper the graph becomes once the distance of $x$ from $0$ exceeds $1$.
This task could profitably be combined with graphing technology. The calculator can produce accurate graphs readily and then the teacher can prompt the students to reflect on the shapes of the graphs, the intersection points, and the important mathematics behind the relative shapes of the graphs.
Solution
-
The functions $f(x) = x^2$ and $g(x) = x^4$ both raise the input $x$ to an even power and so only take non-negative values. These functions increase in size as $|x|$ increases so, in the case of $x^2$, we obtain a parabola opening upward. In the case of $x^4$ we get a curve whose shape is also similar to that of a parabola, also opening upward. It is important to note that when $|x| \lt 1$, $|x^4| \lt |x^2|$ because raising to a higher power decreases the size of a number when $|x| \lt 1$. When $|x| \gt 1$, $|x^4|$ is larger than $|x^2|$. Hence the graph of $g(x)$ is closer to the $x$-axis than the graph of $f(x)$ when $0 \lt |x| \lt 1$ and is further from the $x$-axis once $|x| \gt 1$.
To see where the two graphs meet we set $f(x) = g(x)$ and solve: if $x^2 = x^4$ this means that $x^4 - x^2 = 0$. But
\begin{eqnarray} x^4 - x^2 &=& x^2(x^2-1) \\ &=& x^2(x+1)(x-1). \end{eqnarray}So $f(x) = g(x)$ when $x = 0, -1, +1$.
-
In this case, the functions $f$ and $g$ raise $x$ to negative powers. So $f$ and $g$ will take positive values when the input is positive and negative values when the input value is negative. Like in the previous case, the behavior of the two functions when $|x| \lt 1$ is different from when $|x| \gt 1$. Here $g$ raises $x$ to a higher power so $g(x)$ is closer to the $x$ axis than $f(x)$ when $|x| \lt 1$ and for the same reason $g(x)$ is further from the $x$-axis than $f(x)$ when $|x| \gt 1$.
Finding when the two graphs meet, we set $x^3 = x^5$ as above and find
\begin{eqnarray} x^5 - x^3 &=& x^3(x^2-1) \\ &=& x^3(x+1)(x-1) \end{eqnarray}so the two graphs meet when $x = 0, -1, + 1$.

-
In this case $f(x) = x^2$ and $g(x) = x^3$. We have already graphed the function $f$ in part (a) and $g$ in part (b). For positive values of $x$, where both $f$ and $g$ take positive values, $f$ takes larger values then $g$ when $0 \lt |x| \lt 1$ and smaller values once $x \gt 1$.
\begin{eqnarray} x^3 - x^2 &=& x^2(x-1) \\ &=& x^2(x-1) \end{eqnarray}so the two graphs meet when $x = 0, + 1$.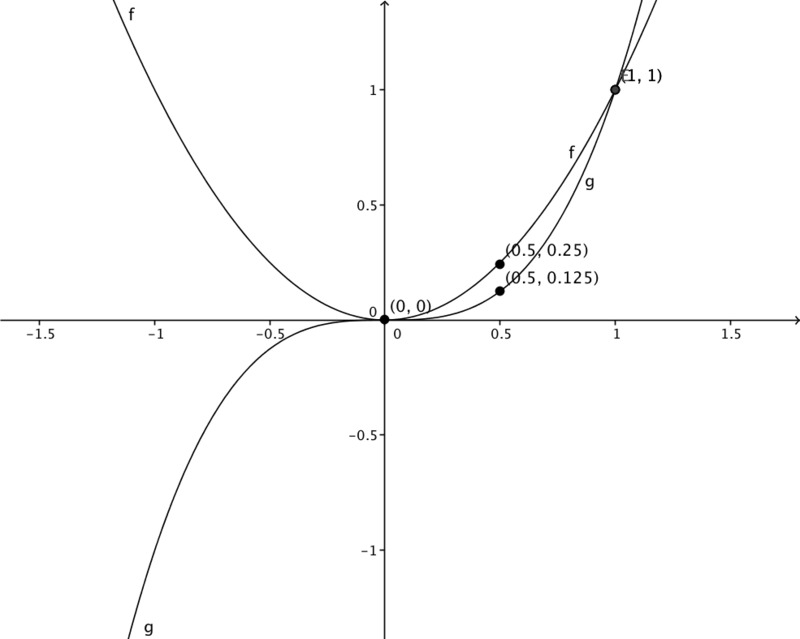
Graphs of Power Functions
Sketch the graphs of the functions described by $\displaystyle f(x)=x^2$ and $\displaystyle g(x)=x^4$ on the same axes, being careful to label any points of intersection. Also, find and label $\displaystyle\left(\frac{1}{2}, f(\frac{1}{2})\right)$ and $\displaystyle\left(\frac{1}{2}, g(\frac{1}{2})\right)$.
Sketch the graphs of the functions described by $f(x)=x^3$ and $g(x)=x^5$ on the same axes, being careful to label any points of intersection. Also, find and label $\displaystyle\left(\frac{1}{2}, f(\frac{1}{2})\right)$ and $\displaystyle\left(\frac{1}{2}, g(\frac{1}{2})\right)$.
Sketch the graphs of the functions described by $f(x)=x^2$ and $g(x)=x^3$ on the same axes, being careful to label any points of intersection. Also, find and label $\displaystyle\left(\frac{1}{2}, f(\frac{1}{2})\right)$ and $\displaystyle\left(\frac{1}{2}, g(\frac{1}{2})\right)$.
