Bank Shot

Task

Pablo is practicing bank shots on a standard 4 ft.-by-8 ft. pool table that has a wall on each side, a pocket in each corner, and a pocket at the midpoint of each eight-foot side.

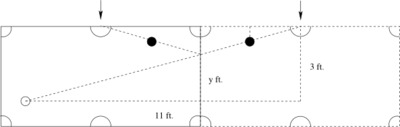
Pablo places the cue ball one foot away from the south wall of the table and one foot away from the west wall, as shown in the diagram below. He wants to bank the cue ball off of the east wall and into the pocket at the midpoint of the north wall.

1. At what point should the cue ball hit the east wall?
2. After Pablo practices banking the cue ball off of the east wall, he tries placing the eight-ball two feet from the east wall, as shown in the diagram below, so that if he shoots the cue ball exactly as he did before, the cue ball will strike the eight-ball directly and sink the eight-ball into the north pocket. How far from the north wall should Pablo place the eight-ball?

IM Commentary

Standard G-SRT.5 calls for students to "use congruence and similarity criteria for triangles to solve problems." This task asks students to use similarity to solve a problem in a context that will be familiar to many, though most students are accustomed to using intuition rather than geometric reasoning to set up the shot.

In order to solve this problem, students must use the fact that when an object bounces off of a wall, the angle of incidence equals the angle of reflection; that is, the angle at which the object hits the wall is equal to the angle at which the object ricochets from the wall. Students who have not taken a physical science course may need to be given this fact (or asked to conjecture it after thinking about several examples of collisions).

Solutions

Solution: Solution 1

1. Let $x$ be the distance from the northeast corner of the table at which Pablo wants the cue ball to hit the east wall. We start by drawing two right triangles as shown in the diagram above: one whose hypotenuse is the segment from the desired point of contact with the east wall to the north pocket, and one whose hypotenuse is the segment from the cue ball to the point of contact with the east wall. The former right triangle has legs of length 4 ft. and $x$ ft.; the latter has legs of length 7 ft. (because the cue ball begins one foot away from the west wall) and $(3 - x)$ ft. (because it begins one foot away from the south wall).

   Because the angle at which the cue ball hits the wall is equal to the angle at which it rebounds off of it, and because the two right triangles already have one right angle each, we know the two triangles are similar by AA similarity, and therefore $$ \frac{7}{(3 - x)} = \frac{4}{x}. $$ Multiplying each side by $x(3 - x)$ yields $$7x = 4(3 - x)$$ and we obtain $x = \frac{12}{11}$ ft. Therefore, Pablo wants the cue ball to contact the east wall $\frac{12}{11}$ ft. away from the northeast corner of the table.



2. Suppose we form another right triangle by drawing the perpendicular from the eight-ball to the north wall. This produces a right triangle that is similar to the one in the upper-right corner of the table. Since the foot of the perpendicular is 2 ft. away from the north pocket, the scale factor between the two triangles is $\frac12$. So the eight-ball should be placed half of $\frac{12}{11}$ ft., or $\frac{6}{11}$ ft., away from the north wall.

Solution: Solution 2

This alternative solution uses a clever strategy in which we picture the reflection of the pool table across the east wall. Because the angle of incidence is equal to the angle of reflection when the cue ball collides with the east wall, if we reflect the continuation of the ball's trajectory across the east wall, this reflection will form a straight line with the ball's initial trajectory. We can use this fact to determine exactly where the cue ball should "cross" the east wall in this diagram. (In fact, if a pool table came with mirrors on each wall, Pablo could use this strategy to aim his shot perfectly, since he could simply direct his shot at the north pocket's reflection in the east wall mirror.)

1. We draw a right triangle whose hypotenuse is the segment from the cue ball to the reflection of the north pocket. The legs of this right triangle are 7 ft. + 4 ft. = 11 ft. and 3 ft., since the cue ball starts one foot away from the west wall and one foot away from the south wall. Let the distance from the desired point of contact with the east wall and the horizontal leg of this right triangle be $y$ feet. Then our right triangle contains another, similar right triangle (by AA similarity) whose legs have length $y$ ft. and 7 ft. Therefore, the scale factor between this smaller triangle and the original right triangle is $\frac{7}{11}$. To compute $y$, then, we multiply 3 by $\frac{7}{11}$ to get $\frac{21}{11}$. Thus the ball should hit the east wall $\frac{21}{11}$ ft. north of the horizontal dotted line in the diagram. This is $3 - \frac{21}{11} = \frac{12}{11}$ feet away from the northeast corner pocket.



2. We draw a perpendicular from the reflection of the eight-ball's desired position to the reflection of the north wall. With the reflection of the north wall, this perpendicular forms a right triangle that is similar to the one with legs of 3 feet and 11 feet by AA similarity (using the fact that the smallest angle of the new triangle and the smallest angle of the old triangle are alternate interior angles for two parallel horizontal lines). The horizontal leg of the new triangle has length 2 feet, so the scale factor between the two triangles is $\frac{2}{11}$. So to compute the length of the perpendicular from the reflection of the eight-ball to the reflection of the north wall, we multiply 3 feet by $\frac{2}{11}$ to get $\frac{6}{11}$ feet. Thus the eight-ball should be placed $\frac{6}{11}$ feet away from the north wall.