Zeroes and factorization of a non polynomial function
Task
- Sketch graphs of the functions $f$ and $F$ given by $f(x)= |x|$ and $F(x) = x^2$ for $-2 \leq x \leq 2$.
- Suppose $g$ is the function given by $g(x) = \frac{f(x)}{x}$ for $x \neq 0$ and $G$ is the function given by $G(x) = \frac{F(x)}{x}$ for $x \neq 0$. Sketch graphs of the functions $g$ and $G$ for $x \neq 0$ and $-2 \leq x \leq 2$.
- Is there a natural way to define $g$ and $G$ when $x =0$? Explain.
IM Commentary
For a polynomial function $f$, if $f(0) = 0$ then the polynomial $f(x)$ is divisible by $x$. This fact is shown and then generalized in ''Zeroes of a quadratic polynomial I, II'' and ''Zeroes of a general polynomial.'' Here, divisibility tells us that the quotient $\frac{f(x)}{x}$ will still be a nice function -- indeed, another polynomial, save for the missing point at $x=0$. The goal of this task is to show via a concrete example that this nice property of polynomials is not shared by all functions. The non-polynomial function $F$ given by $F(x)=|x|$ is a familiar function for which property does not hold: even though $F(0)=0$, the quotient $\frac{F(x)}{x}$ behaves badly near $x=0$. Indeed, its graph is broken into two parts which do not connect at $x = 0$.
The level of the task is appropriate for assessment but since its intention is to provide extra depth to the standard A-APR.2 it is principally designed for instructional purposes only. The students may use graphing technology: the focus, however, should be on what happens to the function $g$ when $x = 0$ and the calculator may or may not be of help here (depending on how sophisticated it is!).
Solution
-
Below is a picture of the graph of the equation $y = |x|$ when $-2 \leq x \leq 2$: it is the graph of the equation $y = x$ when $0 \leq x \leq 2$ and the graph of the equation $y = -x$ when $-2 \leq x \leq 0$.

Below is a picture of the graph of the equation $y = x^2$ when $-2 \leq x \leq 2$:

-
If $g$ satisfies $g(x) = \frac{f(x)}{x}$ this means that $g(x) = \frac{|x|}{x}$. When $x \gt 0$ we have $|x| = x$ and so in this case $$ g(x) = \frac{x}{x} = 1. $$ Similarly, if $x \lt 0$ then $|x| = -x$ and so $$ g(x) = \frac{-x}{x} = -1. $$ Below is a graph of the function $y = g(x)$:
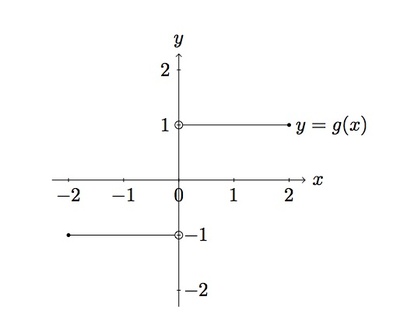
If $G$ is a function which satisfies $G(x) = \frac{F(x)}{x}$ this means that $G(x)= \frac{x^2}{x} = x$. The graph of $G$ is shown below for $-2 \leq x \leq 2$ and $x \neq 0$:

-
The graph of $g$ is broken into two parts which do not come together when $x = 0$. To the right of $x = 0$, $g$ always takes the value $1$ while to the left of $x = 0$, $g$ always takes the value $-1$. Coming from the left $g$ appears as if it will take the value $-1$ when $x = 0$ while coming from the right it appears as if $g$ will take the value $1$ when $x = 0$. There is no ''natural'' choice for what value $g$ should take when $x=0$.
Unlike $g(x)$, the function $G(x)$ looks exactly like the function $h(x) = x$ except that the point $(0,0)$ is missing. This makes sense because $$ G(x) = \frac{x^2}{x} = x $$ and the only problem with $G$ is that it has been expressed with an $x$ in the denominator so that it is not defined when $x = 0$. Looking at the graph of $G$, however, it is natural to define $G(0) = 0$.
Zeroes and factorization of a non polynomial function
- Sketch graphs of the functions $f$ and $F$ given by $f(x)= |x|$ and $F(x) = x^2$ for $-2 \leq x \leq 2$.
- Suppose $g$ is the function given by $g(x) = \frac{f(x)}{x}$ for $x \neq 0$ and $G$ is the function given by $G(x) = \frac{F(x)}{x}$ for $x \neq 0$. Sketch graphs of the functions $g$ and $G$ for $x \neq 0$ and $-2 \leq x \leq 2$.
- Is there a natural way to define $g$ and $G$ when $x =0$? Explain.
