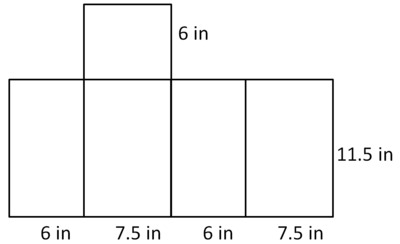
Christo’s Building
Christo and Jeanne Claude are artists who wrap large things – bridges, buildings, even islands. (See www.christojeanneclaude.net for images.)
Imagine that Jean Claude and Christo are preparing for their next large project – that of wrapping a large building. They are building a scale model in order to plan out the project.
The model building will measure $11 \frac12$ inches high, and $7 \frac12$ inches wide, and 6 inches long.
They are considering building the model with blocks that measure $\frac12 \text{ in}$ on each side.
-
What is the volume of the building in cubic inches?
-
How many of the blocks that measure $\frac12 \text{ in}$ on each side would Jeanne Claude and Christo need to make the model building?
-
Draw a picture of the model building and determine how much fabric Jean Claude and Christo will need to cover the model building.
-
The way Jean Claude and Christo have made their model, they know that they the number of square feet needed to cover the real building is 144 times the number of square inches needed to cover the model. How much fabric will Jean Claude and Christo will need to cover the real building?

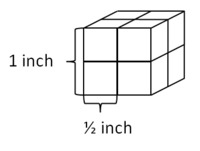 Every cubic inch of volume requires 8 cubes, so we can think of a cubic inch as a group of 8 smaller cubes). Since the volume is given in cubic inches, we multiply the volume by 8: $$517.5\times8=4140$$
So they would need 4140 of the blocks to make the model.
Every cubic inch of volume requires 8 cubes, so we can think of a cubic inch as a group of 8 smaller cubes). Since the volume is given in cubic inches, we multiply the volume by 8: $$517.5\times8=4140$$
So they would need 4140 of the blocks to make the model.