Olympic Men's 100-meter dash
The scatterplot below shows the finishing times for the Olympic gold medalist in the men's 100-meter dash for many previous Olympic games. The line of best fit is also shown. (Source: http://trackandfield.about.com/od/sprintsandrelays/qt/olym100medals.htm)
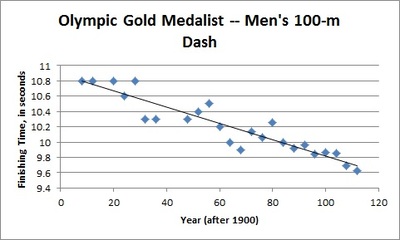
- Is a linear model a good fit for the data? Explain, commenting on the strength and direction of the association.
- The equation of the linear function that best fits the data (the line of best fit) is $$\widehat{\mbox{Finishing time}} = 10.878 - 0.0106 \left( \mbox{Year after 1900} \right).$$ Given that the summer Olympic games only take place every four years, how should we expect the gold medalist's finishing time to change from one Olympic games to the next?
- What is the vertical intercept of the function's graph? What does it mean in context of the 100-meter dash?
- Note that the gold medalist finishing time for the 1940 Olympic games is not included in the scatterplot. Use the model to estimate the gold medalist's finishing time for that year.
- What is a realistic domain for the linear function? Comment on how your answer pertains to using this function to make predictions about future Olympic 100-m dash race times.
