Summer Intern

Task

You have been hired for a summer internship at a marine life aquarium. Part of your job is diluting brine for the saltwater fish tanks. The brine is composed of water and sea salt, and the salt concentration is 15.8% by mass, meaning that in any amount of brine the mass of salt is 15.8% of the total mass.

1. The supervisor asks you to add fresh water to one liter of the brine using a half-liter measuring cup. Let $S(x)$ be the salt concentration of the resulting mixture when you add $x$ half-liters of salt. Write an expression for $S(x)$. [Assume that one liter of water has mass 1 kg.]
2. Describe how the graph of $S$ is related to the graph of $y = 1/x$.
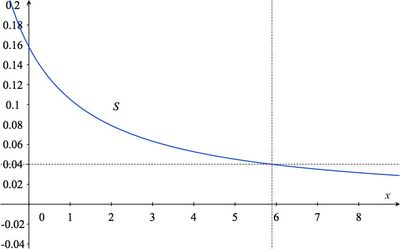
3. Sketch the graph of $S$.
4. How much fresh water should you add to get a mixture which is 4% sea salt, approximately the salt concentration of the ocean?

Solutions

Solution: Summer Intern

1. Because the brine is 15.8% sea salt, the initial salt concentration is $$\frac{\mbox{0.158 kilograms of salt}}{\mbox{1 kilogram of brine}}.$$ Adding $x$ half-liters of water is the same as adding $x$ half-kilograms of mass. This increases the total mass of the mixture by the $x$ half-kilograms, to $0.5x+1$, while leaving the mass of salt unchanged. So an expression for $S(x)$ is $$\frac{0.158}{0.5x+1}$$
2. We write the expression for $S(x)$ in a form that shows its relation with $1/x$: $$\frac{0.158}{0.5x+1} = \frac{0.158}{0.5(x+2)} = \frac{0.316}{ x+2} = 0.316 \frac{1}{x+2}.$$ Thus $S(x)$ is obtained from $1/x$ by first replacing $x$ with $x+2$ and then multiplying the whole by $0.316$. So the graph of $S$ is the graph of $$y={1\over x}$$ horizontally translated by $2$ units to the left, and vertically dilated by $0.316$ units.
3. 
   
4. Since a solution which is 4% sea salt has a salt concentration of $0.04$, we must find $x$ satisfying $S(x) = 0.04$. So, we solve the equation $\displaystyle{0.316\over x+2}=0.04$ for $x$: \begin{eqnarray*} {0.316\over x+2}&=&0.04\\ 0.316&=&0.04 (x+2)\\ \frac{0.316}{0.04}&=&x+2\\ 7.9&=&x+2\\ 5.9&=&x. \end{eqnarray*} So to each liter of 15.8% brine we would have to add about 6 half-liters of fresh water (3 liters) in order to get a 4% sea salt solution.

Solution: A tabular approach to part (d)

Using a calculator or spreadsheet we construct a table of values of $S(x)$ from the expression for $S(x)$ found in (b):

Number of half-liters	Salt concentration
0	0.158
1	0.153
2	0.079
3	0.0632
4	0.0527
5	0.045
6	0.0395
7	0.035

The table shows that the salt concentration is very close to 4% when 6 half-liters (3 liters) of fresh water are added to the brine.

Solution: A graphical approach to part (d)

The solution to part (d) can be estimated from the graph found in (c) by drawing a horizontal line with vertical coordinate 0.04 and seeing what the value of $x$ is where it intersects the graph of $S$: