Linear Functions

Task

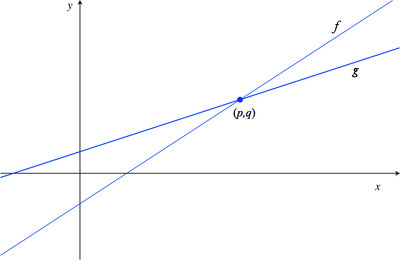
The figure below shows the graphs of the functions represented by $f(x)=4x-a$ and $g(x)=2x+b$ for some constants $a$ and $b$. They intersect at the point $(p,q)$.

1. Label the graph of $f$. Do the same for the graph of $g$.
2. What do $a$ and $b$ represent in the graphs above?
3. Imagine you place the tip of your pencil at point $(p,q)$ and trace the graph of $f$ out to the point with $x$-coordinate $p+2$. Imagine I do the same on the graph of $g$. How much greater would the $y$-coordinate of your ending point be than mine?

IM Commentary

This task requires students to use the fact that on the graph of the linear function $h(x)=ax+b$, the $y$-coordinate increases by $a$ when $x$ increases by one. Specific values for $a$ and $b$ were left out intentionally to encourage students to use the above fact as opposed to computing the point of intersection, $(p,q)$, and then computing respective function values to answer the question.

Solution

1. 
   Because the slope of the graph of $f$, $4$, is greater than the slope of the graph of $g$, $2$, we label the steeper line $f$ and the other $g$.

2. $-a$ is the $y$-coordinate of the point where the graph of $f$ intersects the $y$-axis. $b$ is the $y$-coordinate of the point where the graph of $g$ intersects the $y$-axis.
3. Since the graph of $f$ has slope $4$, each increase of one unit in the $x$-value produces an increase of 4 units in the $y$-value. Thus an increase of 2 units in the $x$-value produce an increase of $2 \cdot 4 = 8$ units in the $y$-value. Since the graph of $g$ has slope 2, an increase of 1 unit in the $x$-value produces an increase of 2 units in the $y$-value. Thus an increase of 2 units in the $x$-value produces an increase of $2\cdot2=4$ units in the $y$-value.

   Thus your $y$-value would be $8–4=4$ units larger than my $y$-value.