As the Wheel Turns

Task

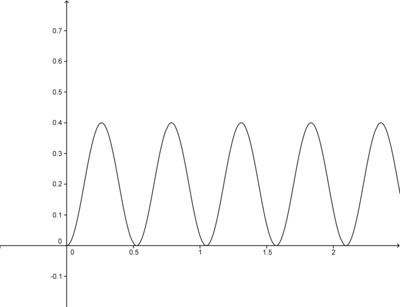
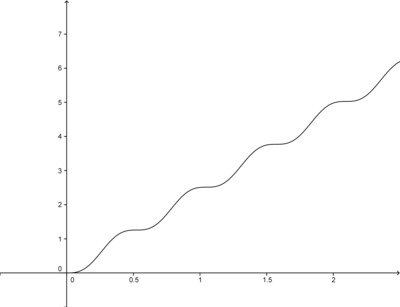
A wheel of radius 0.2 meters begins to move along a flat surface so that the center of the wheel moves forward at a constant speed of 2.4 meters per second. At the moment the wheel begins to turn, a marked point $P$ on the wheel is touching the flat surface.

1. Write an algebraic expression for the function $y$ that gives the height (in meters) of the point $P$, measured from the flat surface, as a function of $t$, the number of seconds after the wheel begins moving.
2. Sketch a graph of the function $y$ for $t>0$. What do you notice about the graph? Explain your observations in terms of the real-world context given in this problem.
3. We define the horizontal position of the point $P$ to be the number of meters the point has traveled forward from its starting position, disregarding any vertical movement the point has made. Write an algebraic expression for the function $x$ that gives the horizontal position (in meters) of the point $P$ as a function of $t$, the number of seconds after the wheel begins moving.
4. Sketch a graph of the function $x$ for $t>0.$ Is there a time when the point $P$ is moving backwards? Use your graph to justify your answer.

IM Commentary

In this task, students use trigonometric functions to model the movement of a point around a wheel and, in the case of part (c), through space (F-TF.5). Students also interpret features of graphs in terms of the given real-world context (F-IF.4).

In order to complete part (a), students must use the linear speed of the wheel to determine its angular speed, and use the unit circle definitions of trigonometric functions (or judicious guessing) to construct a function that gives the vertical position of the point P. In part (c), students must use similar ideas to write a function for the horizontal position of the point P with respect to the center of the wheel, and then combine this with the horizontal position of the center of the wheel to obtain the point's horizontal position with respect to the starting point. The difficulty of the task likely makes it more appropriate for groupwork than as an individual exercise.

Solution

1. Since we are currently interested only in the vertical position of the point $P$, we can ignore the fact that the wheel is moving horizontally and pretend that the center of the wheel is stationary. To find an expression for $y(t)$, we start by defining $\theta$ to be the angle shown below:
   
   
   Since the wheel moves at a speed of 2.4 m/s, and the circumference of the wheel is $2\pi r = 0.4 \pi$ meters, the wheel completes $\frac{2.4}{0.4 \pi} = \frac{6}{\pi}$ rotations per second. This means that $\theta$ is increasing at a rate of $\frac{6}{\pi} \cdot 2\pi = 12$ radians per second. So $\theta = 12t$, where $t$ is the time in seconds after the wheel begins to move.
   
   We observe that the height of the point P is equal to 0.2 meters, the height of the center of the wheel, plus or minus the vertical part of the radius from the center of the wheel to P. The vertical part of the radius is $0.2 \cos \theta = 0.2 \cos (12t)$, so the height of the point P is given by $$ y(t) = 0.2 - 0.2 \cos(12t). $$
2. 
   
   Graphing the function $y(t)$, we notice that the graph of the function touches the line $y = 0$ but does not go below this line. This makes sense in terms of the real-world context, because the height of the point $P$ reaches zero but does not go below zero, since the point $P$ never goes beneath the surface.
3. If we pretend temporarily that the center of the wheel is stationary, we can use our finding from part (a) that $\theta = 12t$ to show that the horizontal position of the point $P$, with respect to the center of the circle, is $- 0.2\sin(12 t)$. (This is because the length of the horizontal part of the radius from the center to point $P$ is $0.2 \sin(12 t)$, and this part initially points to the left.)
   
   Now we take into account the horizontal motion of the center of the wheel. Since the center is advancing at a rate of 2.4 meters per second, the horizontal position of the point $P$ is equal to $$ x(t) = 2.4 t - 0.2 \sin(12 t). $$
4. 
   
   

   Note that the scale for this graph is not the same as the scale for the graph given in part (b).

   To determine whether the point $P$ ever moves backwards, we look at the graph of $x(t)$ to see whether $x$ ever decreases. The graph suggests that $x$ does not decrease, though there are points at which the graph is momentarily horizontal. At the times corresponding to these points, the horizontal movement of $P$ has momentarily slowed to a halt. If we put the graphs of $x(t)$ and $y(t)$ on the same set of axes, we can also observe that the times when $P$ stops advancing horizontally are the same times when $P\,$ touches the surface.